Треугольник

Индивидуальное значение

Тату «треугольник» для каждого человека является чем-то особенным

Так, например, для девушек эта простая на вид фигура, может означать кое-что важное и глубокомысленное. Треугольник – отображение трех циклов жизни практически любой женщины

Это девичество, материнство и старость. Не все могут додуматься до такого. Однако подобное разъяснение существует уже давно, и многие набивают треугольник намеренно с этой целью.

Для мужчин же фигура означает кое-что другое. Треугольник также символизирует «троицу», однако в данном случае это не цикл жизни, а качества. Если быть точнее, то мудрость, сила и красота

К слову, очень важно, какой был выбран участок для татуировки. Он способен усилить, подчеркнуть придаваемый смысл

Чаще всего такие тату можно видеть на запястье, предплечье или на затылке. Это самые популярные варианты исполнения. Но на самом деле человек сам выбирает место.

Иногда треугольники закрашивают. Цвет также означает очень многое. Красный символизирует страсть, черный – негатив, зеленый – безопасность, оранжевый – жизнелюбие. Оттенок действительно может рассказать о многом, так что выбирать его нужно особенно тщательно. И, кстати, стоит учитывать, что на коже выбранный цвет всегда смотрится на 2-3 тона темнее. Следует об этом знать и подбирать краску с осознанием данного факта.

Виды треугольников

В зависимости от величин углов и соотношения длин сторон различают следующие виды треугольников.

Виды треугольников по углам:

• остроугольные
• прямоугольные
• тупоугольные

Остроугольный треугольник — это треугольник, все углы которого острые (то есть градусная мера каждого угла меньше 90º).

Прямоугольный треугольник — это треугольник, у которого один угол прямой (то есть имеет градусную меру 90º).

Тупоугольный треугольник — это треугольник, у которого один угол — тупой (то есть имеет градусную меру больше 90º).

Виды треугольников по сторонам:

• равносторонние
• равнобедренные
• разносторонние

Равносторонний треугольник (или правильный треугольник) — это треугольник, у которого все три стороны равны.

Равнобедренный треугольник — это треугольник, у которого две стороны равны.

Разносторонний треугольник — треугольник, все стороны которого имеют разную длину.

Если в задаче ничего не сказано о виде треугольника, его считают произвольным, то есть разносторонним.

Отрезки равной длины на чертеже отмечают равным количеством черточек:

разносторонний треугольник

равносторонний треугольник

равнобедренный треугольник

Равенство треугольников

Случаются ситуации, когда точно известно, что два треугольника равны, а что же в таком случае можно сказать про углы и стороны таких треугольников?

Нам дано: ∆ABC = ∆A₁B₁C₁. Равны ли соответствующие стороны и углы данных фигур?

По условию треугольники равны. Значит, применяем рассмотренное правило, которое говорит о том, что все соответствующие элементы фигуры равны между собой.

Получается:

Если ∆ABC = ∆A₁B₁C_1, то равны соответствующие стороны:

АС =А₁С₁;

АВ = А₁В₁;

СВ = С₁В₁;

и соответствующие углы равны:

∠С =∠С₁;

∠А = ∠А₁;

∠В = ∠В_1.

Геометрия интересна тем, что большинство её правил нуждаются в доказательствах. Такие правила называют теоремами.

Вместе с этим, имеются и самостоятельные правила, которые называют аксиомами геометрии.

Сегодня мы рассмотрим первую теорему с названием «Первый признак равенства треугольников», и проведем работу по сбору доказательств для данной теоремы.

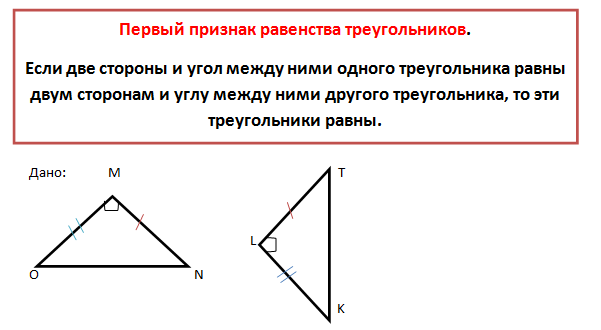
Два треугольника – ∆OMN и ∆KLT. Известно, что две стороны треугольников и угол между ними равны.

Значит:

OM=KL, 

MN=LT;

∠M =∠L.

Докажем, что ∆OMN=∆KLT.

Доказательство первого признака равенства треугольников:

Из условия нам известно, что соответствующие углы равны ∠M =∠L, следовательно, мы можем выполнить наложение двух треугольников так, чтобы вершина M совпадала с вершиной L.

Тогда, сторона OM наложится на сторону  KL, а сторона MN на отрезок LT. По условию нам известно, что отрезки равны OM=KL, MN=LT, значит, при наложении они совпадут. Получается, что при наложении совпадает угол, и две стороны, следовательно, будут совпадать и оставшиеся стороны ON и KT, то есть ON = KT . Если при наложении совмещаются три стороны и одна вершина, значит, совместятся и две другие вершины KO и TN.

Выходит, что при совмещении совпадают все элементы ∆, а такие ∆ называются равными.

Мы доказали, что ∆OMN=∆KLT.

Еще, нам предстоит познакомиться с несколькими понятиями, без которых продолжать изучение  геометрии невозможно.

Начертим прямую АВ. Выберем точку не лежащую на данной прямой. Проведем отрезок СК, соединяющий точку С и прямую АВ, таким образом, чтобы при пересечении СК и АВ образовывался прямой угол (90˚) . Изображенный отрезок СК называют перпендикуляром к прямой.

Доказательство будем проводить в два этапа.

1 этап

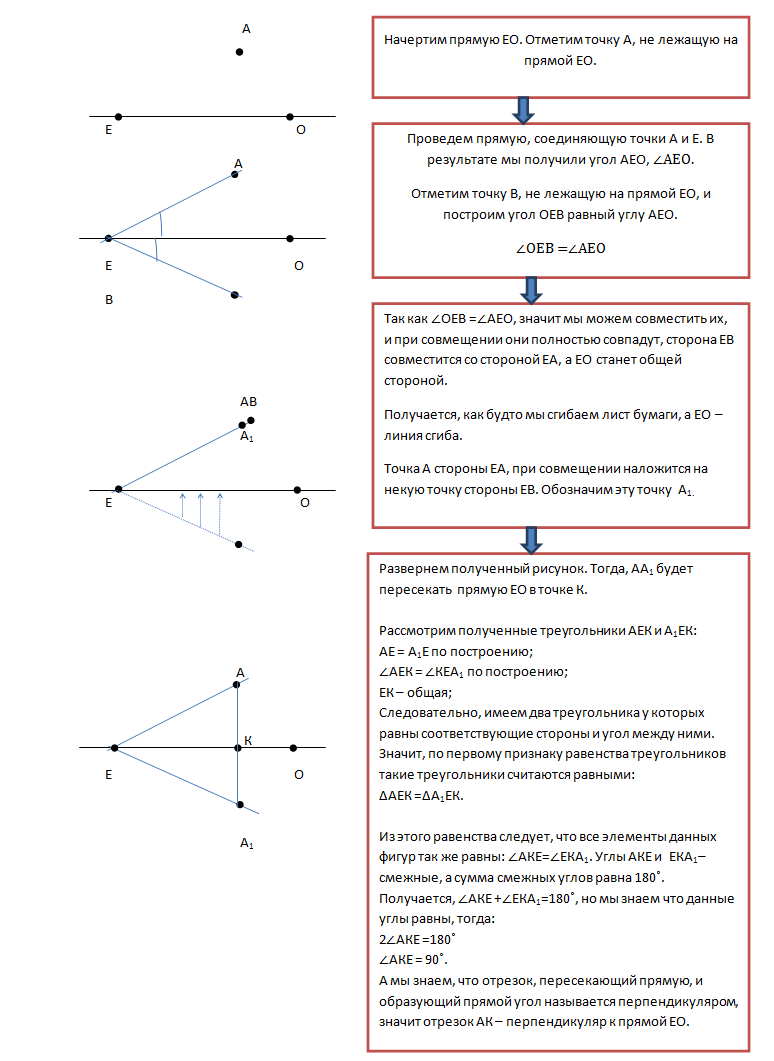2 этап

Теорема доказана.

Какие бывают геометрические фигуры?

Какие бывают геометрические фигуры?

• В сферу изучения науки геометрии входят плоские (двухмерные) фигуры и объмные фигуры (трхмерные).

  Из плоских:

  Их изучает планиметрия. Точка тоже плоская фигура.

  Из объмных известны:

  Их изучает стереометрия.

• К фигурам также относится и точка.

  Трехмерные фигуры — куб, сфера, полусфера, конус, цилиндр, пирамида, параллелепипед, призма, эллипсоид, купол, тетраэдры и множество других, выходящие из вышеуказанных. Далее идут очень сложные геометрические фигуры — различные многогранники, которые по сути могут содержать бесконечное количество граней. Например, большая клинокорона — состоит из 2-х квадратов и 16-ти правильных треугольников или клинокорона, составленная из 14 граней: 2 квадрата и 12 правильных треугольника.

• Говоря о геометрических фигурах, можно выделить такие две закономерные группы как:

  1) Двухмерные фигуры;

  2) И трхмерные фигуры.

  Итак, поподробнее о двухмерным, к ним можно отнести такие фигуры как:

  А вот что касается трхмерных фигур, то вот какими они могут быть:

• Очертания фигур и все возможные действия с ними изучают математические науки геометрия (изучает плоские фигуры) и стереометрия (предмет изучения — объемные фигуры). Я в школе любила и ту, и другую науку.

  Вот так классифицируются плоские (2D) фигуры:

  **

  Объемные фигуры (3D) классифицируются таким образом:

  **

  Это куб, параллелепипед, тетраэдр, цилиндр, пирамида, икосаэдр, шар, додекаэдр, конус, октаэдр, призма, сфера. К тому же есть усеченные фигуры (пирамида, конус). В зависимости от основания, пирамида, призма делятся на треугольные, четырехгранные и так далее.

  Детские игрушки (пирамидки, мозаика и другие) позволяют с раннего детства знакомить детей с геометрическими объемными фигурами. А плоские фигуры можно нарисовать и вырезать из бумаги.

• Из двухмерных можно назвать следующие:

  • круг;
  • овал;
  • квадрат;
  • прямоугольник;
  • параллелограмм;
  • трапеция;
  • пятиугольник (шестиугольник и т.д.);
  • ромб;
  • треугольник.

  С трехмерными немного посложнее:

  • куб;
  • цилиндр;
  • конус;
  • призма;
  • сфера или шар;
  • параллелепипед;
  • пирамида;
  • тетраэдр;
  • икосаэдр;
  • октаэдр;
  • додекаэдр.

  Думаю многие, прочитав последния названия, спросили про себя: quot;Что-что?quot;. Для наглядности — иллюстрация:

• На самом деле фигур в математике достаточно. Плоские фигуры это — прямоугольники, квадрат, треугольник, пятиугольник, шестиугольник, круг. Объемные фигуры или 3D фигуры — это как пирамида, так и куб и додекаэдр, и тд.

• 1 Из двухмерных фигур:

  2 Из трхмерных фигур:

  Призма, пирамида, параллелепипед, призма, шар (сфера), цилиндр, полусфера (половинка от сферы, то есть шар, разрезанный пополам) и конус. Пирамиды делятся на треугольные, четырхугольные и так далее (почти до бесконечности). Чем больше у пирамиды углов в основании, тем больше она напоминает конус.

• Трхмерные фигуры (3D): двугранный угол, многогранный угол; многогранник (разновидности многогранников: призма разновидности призмы: параллелепипед, куб, антипризма, пирамида разновидность тетраэдр, усечнная пирамида, бипирамида разновидность октаэдр, додекаэдр, икосаэдр, клин, обелиск); цилиндр, усечнный цилиндр, отрезок цилиндра (он же цилиндрическая подковка или quot;копытоquot;), конус, усечнный конус, сфера, шар, шаровой сегмент, шаровой слой, шаровой сектор, эллипсоид, геоид…

• С самого начала мы на уроках геометрии изучаем простые фигуры, которые являются плоскими, то есть располагаются на одной плоскости.

  Далее, перед нами открывается мир объмных фигур, которые необходимо представлять и понимать, как они расположены и как грамотно их нарисовать, чтобы было понятно не только вам, но и окружающим.

  Итак, перечень основных фигур можно изучить ниже.

• В последнее время мне как раз приходилось рассказывать своим внучкам и внуку, какими могут быть геометрические фигуры.

  Начинали с плоских фигурок, вырезанных из картона или сделанные из пластмассы, дети учились различать треугольник и квадрат, овал и круг, прямоугольник, ромб и многоугольник.

  Помогали в запоминании названий фигур и вот такие специальные игрушки с отверстиями определнной формы.

  Позднее перешли на объмные фигурки, кубики и конусы, параллелепипеды, шары и кольца, пирамидки и цилиндры.

  До школы они пока не доросли, а когда пойдут, то их научат различать равнобедренные и равносторонние треугольники, узнают про луч и точку, про окружность и вс остальное.

Что такое треугольник Карпмана в психологии?

Определение треугольник Карпмана и что это значит, впервые появилось в психологии благодаря психотерапевту из Америки, Стивену Карпману и получило название в его честь.

Он раскрыл ещё одну тайну человеческой психики и вывел новую концепцию. Согласно ей, мы играем в своей жизни множество разных ролей, но все они могут быть ограничены тремя образами: Спасатель, Жертва и Палач. Существуют разные названия этих ипостасей, но они сохраняют один и тот же смысл. Суть сводится к конфликту между жертвой и преследователем в присутствии третьего лица.

Треугольник Карпмана — это созависимые отношения, которые возникают из-за потребности самоутвердиться за чужой счёт. Результатом становится манипулирование и эмоциональная разрядка. Но положительное влияние эта схема оказывает не на всех участников. В выигрыше остаётся лишь жертва, а спасатель выходит из игры эмоционально измотанным и опустошённым. Удивительный факт, но провокатора конфликта — злодея и палача, может даже не быть во время развития ситуации. На эту роль выбирают бывшего мужа, начальника и любого другого обидчика.

Треугольник в психологии жертва спасатель преследователь является частым спутником в жизни многих людей. Мы вживаемся во все эти роли, выбирая одну как самую любимую. Реальное положение вещей остаётся за кадром, оно игнорируется. Это всё происходит неосознанно. Возможно, вы удивитесь, узнав себя в этой модели поведения, в прошлом или в настоящем. Роли могут меняться в течение разного времени — часа или минуты.

Эта игра насыщает нас яркими переживаниями, эмоциями. Треугольник Карпмана в психологии часто определяется как хроническое состояние некоторых людей. «Подсаживаясь» на эмоции они находят «партнёров по игре» и попадают в порочный круг. Это входит в привычку и воспринимается как естественный ход вещей, единственно возможный способ существования и построения отношений. Это ловушка, в которую попадают многие эмоционально зависимые люди. Чтобы выбраться из неё, нужно приложить усилия и воспользоваться холодным рассудком и силой воли. Одним словом, включить свой разум.

Треугольник на линиях

Большой треугольник на ладони в хиромантии может располагаться на линиях:

Расположение символа на чертах

Например, фигура, расположившаяся на позиции Ума, укажет на успешного человека, знающего свою цель и способы её достижения

Такие люди живут по своему распорядку дня и отличаются особой организованностью.
Иногда фигура располагается рядом с линией Головы, тогда считается, что человек нашёл свой смысл жизни и движется к истинной цели.
Треугольник иногда находится даже на кончике линии Головы, что дарит невероятный ум и особый склад ума.
Важно, что направление вершин треугольника играет особую роль. Женщина скорее всего удачно выйдет замуж, если угол фигуры смотрит на безымянный палец.

Плохо, когда у фигуры повреждён угол, что символизирует тупик и проблемы с завершением пути.

Направление вершины

Бывает, что и вершина смотрит на холмы пальцев. Если речь идёт о безымянном пальце, то перед вами целеустремлённый и творческий человек, который умеет продумывать все нюансы дела.

Иногда фигура поворачивается в сторону мизинца. В таком случае рекомендуют заняться очищением кармы.

На линии жизни и сердца

Что означает в хиромантии треугольник на руке на линии жизни? Обычно это считается негативным предзнаменованием. Знак указывает на опасность, исходящую от огня.

Как расположены символы

Для людей тридцати лет есть свои дополнительные знаки, указывающие на серьёзную опасность:

• крест или четырёхугольник на малом холме Марса;
• четыре точки на холмах верхнего Марса и Аполлона.

Для людей сорока лет:

• разрыв на линии Сатурна;
• расположенный на холме Венеры треугольник с вершиной, направленной вниз.

Взаимосвязь линий

Линии руки и треугольник обычно тесно связаны. Нахождение рассматриваемой фигуры на позиции, отвечающей за эмоциональную сферу, указывает на человека, склонного к точным наукам.

Какая связь между линиями

Такие люди редко вступают в отношения или брак по любви. Обычно ими движет холодный расчёт, а решение принимается только с учётом выгода и всех нюансов.

Дополнительная информация по теме:

1. На линии судьбы треугольник, что означает?
2. Символ «треугольник» на линии брака – хорошо это или плохо?

Женское тату роза в треугольнике: красивые варианты

Очень часто девушки выбирают для себя изображение в виде треугольника, заполненного цветочными мотивами. Розы – самое распространенное из них

С помощью татуировки роз в треугольнике девушка привлекает к себе внимание. Данная нательная композиция прекрасно смотрится как в маленьком, так и большом формате

Место для расположения татуировки треугольника с розами могут быть самыми различными. Все зависит от выбранного размера. Вообще, значение комбинации треугольника с розой трактуется как женская энергетика. Представительницы прекрасного пола, на теле которых можно увидеть тату с розой в комбинации с треугольником, отличаются особым отношением к художественному искусству, музыке и творчеству в целом.

Общее значение

В общем значении тату треугольника обозначает гармонию. Каждая из вершин треугольника обозначает какое-то составляющее человеческого характера и сущности. Таким образом, зачастую это – разум, физическое тело и душа человека. Работая совместно, считается, что эти три составляющих дополняют друг друга, создавая внутреннюю гармонию человека и пробуждая в нем энергию.

Еще одним частым значением такой тату может послужить жизненный цикл человека. Все просто: вершины треугольника – это этапы жизни, то есть рождение, непосредственно жизнь и смерть. Смысл такой тату в том, что, следуя линиям треугольника, вы все равно приходите к первому этапу жизни – к рождению. Это означает то, что жизнь никогда не останавливается, и когда кто-то умирает, вместо него рождается кто-то другой, и так до бесконечности.

В наше время татуировки делаются еще в качестве увековечивания своей любви к другому человеку. Таким образом, делаются также и парные эскизы треугольников для влюбленной пары, которая уверена в своих чувствах.

С точки зрения психологии, треугольник – это наколка, обозначающая лидерство человека. Человек с такой наколкой никогда не терпит поражений, он точен во всем, что, собственно, может понять из самой татуировки.

Еще одно толкование – благосостояние семьи. Все довольно просто и не требует особых объяснений, поскольку можно четко вывести то, что каждая вершина – мать, отец и дети.

Прямоугольный треугольник

В прямоугольном треугольнике катетами называются две стороны треугольника, которые образуют прямой угол. Гипотенузой называется сторона, лежащая напротив прямого угла. 

Некоторые свойства прямоугольного треугольника:

1. Сумма острых углов в прямоугольном треугольнике равна $90$ градусов.
2. Если в прямоугольном треугольнике один из острых углов равен $45$ градусов, то этот треугольник равнобедренный.
3. Катет прямоугольного треугольника, лежащий напротив угла в $30$ градусов, равен половине гипотенузы. (Этот катет называется малым катетом.)
4. Катет прямоугольного треугольника, лежащий напротив угла в $60$ градусов, равен малому катету этого треугольника, умноженному на $√3$.
5. Медиана прямоугольного треугольника, проведенная к его гипотенузе, равна ее половине и радиусу описанной окружности $(R)$. (Рис.14)
6. Медиана прямоугольного треугольника, проведенная к его гипотенузе, делит треугольник на два равнобедренных треугольника, основаниями которых являются катеты данного треугольника. (Рис.14)

Один острый угол прямоугольного треугольника на $44°$ больше другого острого угла. Найдите больший острый угол.

Решение:

В прямоугольном треугольнике $АВС$ $∠А$ и $∠В$ – острые.

Пусть $∠ А – х$, тогда $∠ В — (х+44)$.

Сумма острых углов в прямоугольном треугольнике равна $90$ градусов.

На основании этого правила, составим и решим уравнение:

$х+х+44=90$

$2х+44=90$

$2х=90-44$

$2х=46$

$х=23$

Угол $В$ больший в этом треугольнике, через $«х»$ он записывался как, $х+44$, следовательно, $∠В=23+44=67°$.

Ответ: $67$

Теорема Пифагора

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы. 

$АС^2+ВС^2=АВ^2$

Соотношение между сторонами и углами в прямоугольном треугольнике:

В прямоугольном треугольнике $АВС$, с прямым углом $С$ 

Для острого угла $В$: $АС$ — противолежащий катет; $ВС$ — прилежащий катет.

Для острого угла $А$: $ВС$ — противолежащий катет; $АС$ — прилежащий катет.

1. Синусом $(sin)$ острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
2. Косинусом $(cos)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
3. Тангенсом $(tg)$ острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
4. Котангенсом $(ctg)$ острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.
5. Основное тригонометрическое тождество: $sin^2x+cos^2x=1$
6. В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.
7. Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.
8. Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения.

Значения тригонометрических функций некоторых углов:

$α$	$30$	$45$	$60$
$sinα$	${1}/{2}$	${√2}/{2}$	${√3}/{2}$
$cosα$	${√3}/{2}$	${√2}/{2}$	${1}/{2}$
$tgα$	${√3}/{3}$	$1$	$√3$
$ctgα$	$√3$	$1$	${√3}/{3}$

их разности ( a < b + c, a > b – c; b < a + c, b > a – c; c < a + b, c > a – b ).

Признаки равенства
треугольников.

Треугольники равны, если у них
соответственно равны:

a) 
две стороны и угол между ними;

b) 
два угла и прилегающая к ним сторона;

c) 
три стороны.

Признаки равенства прямоугольных треугольников. 

Два прямоугольных треугольника равны, если
выполняется одно из следующих условий:

1)  равны их катеты;

2)  катет и гипотенуза одного треугольника равны катету и гипотенузе другого;

3)  гипотенуза и острый угол одного треугольника равны гипотенузе и острому углу
другого;

4)  катет и прилежащий острый угол одного треугольника равны катету и
прилежащему острому углу другого;

5)  катет и противолежащий острый угол одного треугольника равны катету и
противолежащему
острому углу другого.

Замечательные линии и точки в
треугольнике.

Высота
треугольника — этоперпендикуляр,опущенный из любой вершины
на противоположную сторону
(
или её продолжение).Эта сторона называетсяоснованием треугольника.Три высотытреугольникавсегдапересекаютсяв одной точке,
называемой ортоцентром треугольника.Ортоцентр остроугольного
треугольника ( точка O,
рис.26 ) расположен внутри треугольника, аортоцентр тупоугольного
треугольника ( точка O,
рис.27 ) – снаружи; ортоцентр прямоугольного треугольника совпадает с
вершиной прямого угла.

Медиана
– это отрезок,
соединяющий любую вершину треугольника с серединой противоположной стороны.Три медианы треугольника
(AD,BE,CF,
рис.28 ) пересекаются в
одной точке
O,
всегда лежащей внутри треугольникаиявляющейсяегоцентром тяжести.Эта точка делит каждую
медиану в отношении 2:1, считая от вершины.

Биссектриса
– этоотрезок биссектрисыуглаот вершины доточкипересечения с противоположной
стороной.
Три биссектрисы треугольника
( AD,
BE,
CF,
рис.29 ) пересекаются в
одной точке О, всегда
лежащей внутри треугольникаиявляющейся центром
вписанного круга (см. раздел «Вписанныеи описанные многоугольники»).

Биссектриса делит противоположную
сторону на части, пропорциональные прилегающим сторонам;
например, на  рис.29  AECE
= ABBC
.

Срединный перпендикуляр
– это перпендикуляр,
проведенный из средней
точкиотрезка(стороны).Три срединных перпендикуляра
треугольника АВС
(KO,
MO,
NO,
рис.30
) пересекаются в одной точке О,
являющейся центром

описанного круга
( точки K,
M,
N
– середины сторон треугольника
ABC
).

В остроугольном треугольнике эта точка
лежит внутри треугольника; в тупоугольном – снаружи; в прямоугольном
-в середине гипотенузы.
Ортоцентр, центр тяжести, центр описанного и
центр вписанного круга
совпадают только в равностороннем
треугольнике.

Теорема Пифагора. В
прямоугольном треугольнике квадрат длиныгипотенузы равен сумме
квадратов длин катетов.

Доказательство теоремы Пифагора с
очевидностью следует из рис.31.
Рассмотрим прямоугольный треугольник
ABCс катетамиa,
bи гипотенузой
c.

Построим квадрат
AKMB,
используя гипотенузу AB
как сторону. Затемпродолжим стороны
прямоугольного треугольника ABC
так, чтобы получить квадрат
CDEF,
сторона которого равна  a+
b
. Теперь ясно, что площадь
квадрата CDEF
равна (a+b)2.
С
другойстороны,этаплощадь равна суммеплощадейчетырёх прямоугольных
треугольников
иквадрата
AKMB,
то есть

c2
+ 4 ( ab
/ 2 ) = c2
+ 2 ab
,

отсюда, 

c2 +
2 ab =( a + b )2 ,

и окончательно имеем:

c2=  a2
+ b2.

Соотношение сторон в
произвольном треугольнике.

В общем случае ( для произвольного
треугольника ) имеем:

c2= a2
+ b2
– 2ab ·cosC,

где
C
– угол между сторонами  a 
и  b
.  

Значение валькнута в качестве татуировки

Татуировку в виде валькнута можно встретить и сейчас. Считается, что такой нательный рисунок указывает своему носителю верный путь.

Это подходит весьма амбициозным личностям, которые готовы жертвовать всем ради познания истины.

Такая татуировка показана людям, очень сильным духом, которые не привыкли сворачивать с выбранного пути.

Кстати, не рекомендуется применять в нательном рисунке валькнут в сочетании с рунами.

Считается, что так он приобретает совершенно ритуальный смысл (примерно как у воинов, идущих «на встречу с Одином»).

Символ «валькнут» имеет общее значение единения миров. Такой талисман помогает проникнуть в тайны мироздания, но одновременно и провоцирует проблемы в жизни носителя.

Преодоление этих невзгод означает, что человек готов к постижению тайных знаний.

Носитель валькнута должен быть очень силен духом и готов к противостоянию жизненным трудностям.

Предыдущая
СкандинавскиеМолот Тора (Мьельнир) — Значение амулета
Следующая
СкандинавскиеСкандинавский оберег шлем ужаса — агисхьяльм

Глупая ошибка строителей

«Египетский треугольник» действительно может помочь в разметке периметра фундамента, однако применение этого метода требует сохранения чётких пропорций. Небольшое отклонение от них − и угол уже не будет прямым. А это приведёт к разнице длин стен. Не единичны случаи, когда при идеальном совпадении длин диагоналей стены получаются разными. Ведь если вдуматься, то трапеция также подходит под заданные параметры, её диагонали равны, в то время как верхняя и нижняя сторона имеют разные длины.

ФОТО: youc.irПравильная трапеция также имеет одинаковые длины диагоналей, однако на квадрат она явно не тянет

Как выглядит треугольник?

В выходной день Глеб с родителями ехали в парк. Мальчик заметил, что вдоль дороги стояла непонятная табличка, увидев которую, отец поехал очень медленно.

«Что это такое?» – поинтересовался ребенок. Папа рассказал, что это дорожный знак, который предупреждает о трудностях на пути. Глебу очень понравился знак, а особенно его форма. Отец продолжил рассказ о знаках: «Форма знака о многом говорит водителю, ведь при плохой видимости автолюбитель видит только форму, а не надпись. Поэтому все предупреждающие знаки – треугольные». «А что такое треугольные?» – не унимался мальчик. Найти ответ на этот и многие другие вопросы папе помог наш сегодняшний урок.

Вначале, давайте разберемся, что же такое треугольник и из чего он состоит.

В повседневной жизни нас окружает масса предметов имеющих треугольную форму. Например:

Часы, воздушный змей, кусочек торта, пиццы, арбуза, салатники, рамки для фотографий, пузырек парфюма – этот список можно продолжать бесконечно. Но что же такое треугольник?

Приведем примеры треугольников:

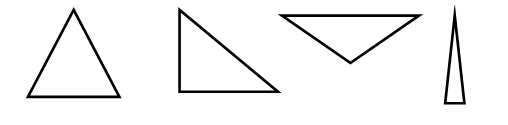
Исходя из определения, каждый рисунок состоит из трех отрезков. В геометрии такие отрезки называют сторонами треугольника.

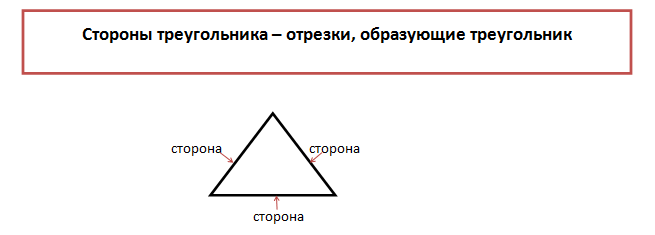
Кроме отрезков, составляющей частью фигуры являются три точки, которые принято называть вершинами.

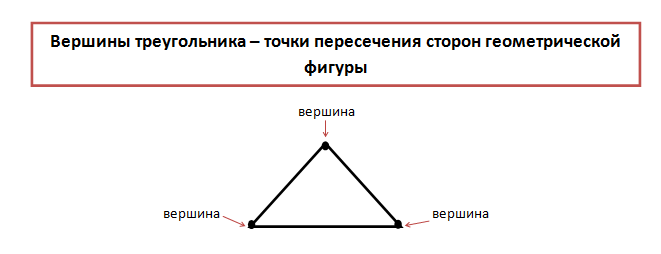
В геометрии, вершины треугольника принято обозначать заглавными буквами латиницы: A,C,D,B.

Начертим треугольник. Вершины, обозначим буквами A,C,D.

Данная геометрическая фигура имеет три вершины A,C,D и три стороны АС, CD, DА.

А как же на письме показать, что данная фигура является треугольником?

Очень интересным является то, что записывать название, можно перечисляя вершины в любом порядке.

Например: 

Можно записать: ∆NOK, ∆OKN, ∆KNО. Каждый вариант записи обозначает один и тот же треугольник и является верным.

Само название фигуры «Треугольник» предполагает, что в состав должны входить три угла. Так ли это?

Внимательно рассмотрим рисунок:

Действительно, мы видим три угла, которые отмечены дугами: ∠RFP,∠FPR, ∠PRF(мы уже знаем, что буква, обозначающая вершину угла всегда записывается в середине) или∠F, ∠P,∠R.

Египетский треугольник в строительстве

Свойства этой уникальной геометрической конструкции заключаются в том, что её построение без применения каких-либо инструментов позволяет построить дом с правильными во всех соотношениях углами.

Итак, качества египетского треугольника позволяют делать правильные во всех соотношениях углы. Стороны конструкции имеют следующее соотношение друг к другу:

Чтобы проверить ту ли фигуру вы начертили, используйте хорошо известную ещё со школьной скамьи Теорему Пифагора.

Для лучшего понимания возьмём приведенную выше зависимость и составим небольшой пример. Умножим пять на пять. В результате чего получим гипотенузу равную 25. Вычислим квадраты двух катетов. Они составят 16 и 9. Соответственно их сумма будет двадцать пять.

Именно поэтому свойства египетского треугольника так часто используются в строительстве. Вам достаточно взять заготовку и прочертить прямую линию. Её длина всегда должна быть кратной 5. Затем нужно наметить один край и отмерять от него линию кратную 4, а от второго 3.

Альтернативные способы построить прямой угол на 90 градусов

Как уже упоминалось выше, наилучшим вариантом будет просто взять угольник или транспортир. Эти инструменты позволяют с наименьшими затратами времени и сил добиться нужных пропорций. Главное же свойство египетского треугольника заключается в его универсальности. Фигуру можно построить, не имея в арсенале практически ничего.

Сильно в построении прямого угла помогают простые печатные издания. Возьмите любой журнал или книгу. Дело в том, что в них соотношение сторон всегда составляет ровно 90 градусов. Типографические станки работают очень точно. В противном случае рулон, который заправляется в станок, будет резаться непропорциональными кривыми углами.

Как получить египетский треугольник при помощи верёвки

Свойства этой геометрической фигуры тяжело переоценить. Неудивительно, что инженерами древности было придумано множество способов её образования с использованием минимальных ресурсов.

Одним из самых простых считается метод образования египетского треугольника со всеми его вытекающими свойствами посредством простой верёвки. Возьмите бечёвку и разрежьте её на 12 абсолютно ровных частей. Из них сложите фигуру с пропорциями 3, 4 и 5.

Как построить угол в 45, 30 и 60 градусов

Безусловно, египетский треугольник и его свойства очень полезны при постройке дома. Но без других углов вам обойтись всё-таки не удастся. Чтобы получить угол, равняющийся 45 градусам, возьмите материал рамки или багета. После чего распилите его под углом в сорок пять градусов и состыкуйте половинки друг с другом.

Как видите, свойства фигуры позволяют гораздо проще и быстрее построить геометрический конструкт. Чтобы добиться соотношения сторон в 60 градусов нужно взять один треугольник на 30º и второй такой же. Обычно подобные пропорции необходимы при создании определённых декоративных элементов.

Свойства египетского треугольника широко использовались в строительстве на протяжении почти, что двух с половиной веков. Даже сейчас при недостатке инструментов строители применяют эту открытую ещё Пифагором методику, чтобы добиться ровных прямых углов.