Как рассчитать площадь комнаты: полезные методики и формулы

Как посчитать периметр комнаты

Периметр — это длина геометрической фигуры по её внешней границе.

Периметр комнаты — это сумма длин сторон комнаты. Соответственно для вычисления периметра необходимо суммировать все стороны.

Формула расчета периметра комнаты:

А — длина комнаты; В — ширина комнаты;

Для комнаты произвольной конфигурации используются более сложные формулы расчета и этот расчет быстрее и удобнее выполнить с применением чертежных программных продуктов.

Быстро выполнить эту простейшую математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.

В нашей проектной организации Вы можете заказать расчет периметра комнаты на основании технологического или конструкторского задания. Расчет выполним для комнаты любой конфигурации по Вашему рисунку с применением самых современных чертежных программ 2D-черчения.

На этой странице представлен самый простой онлайн калькулятор расчета периметра комнаты. С помощью этого калькулятора в один клик вы можете вычислить периметр комнаты, если известны длина и ширина.

Во время ремонта может возникнуть ситуация, когда необходимо знать точный периметр комнаты, например при покупке плинтуса или при расчете количества обоев и напольного покрытия. Сделать это просто, если помещение имеет стандартную форму. Но что делать, если нам нужно произвести расчет для коридора, который имеет множество углов, или для спальни необычной формы? В этом процессе помогут некоторые хитрости, прибегнуть к которым можно при планировании ремонта.

Прямоугольное помещение

Нет ничего проще, чем рассчитать площадь потолка, имеющего прямоугольную форму. Для этого нужно лишь перемножить два параметра комнаты — длину и ширину. Например, площадь потолка, размеры которого: 3 и 4 метра, будет равна 12-ти квадратным метрам (3х4 м).

Вычислить периметр такого потолка тоже весьма просто. Для этого нужно просто сложить длины всех четырех его сторон. В нашем случае периметр потолка будет равен 14 метрам (3+4+3+4 м).

Разумеется, покупая пристенный профиль UD, нужно ориентироваться на то, планки какой длины присутствуют в продаже. Например, если периметр вашего потолка составляет 12,6 метра, а в продаже есть только планки профиля 2-х метровой длины, то вам нужно будет купить не менее семи таких планок.

Как посчитать площадь комнаты в квадратных метрах

Необходимость в расчете площади возникает зачастую только во время ремонтных работ, строительства или при смене мебели. Практически все строительные материалы (например напольное покрытие) исчисляется в квадратных метрах

Для правильного расчета количества материала, важно знать площадь пола. Зная ширину и длину комнаты, найти площадь не вызовет никаких сложностей

Измерения

Перед тем как измерить комнату в квадратных метрах, необходим минимальный набор предметов:

На бумаге необходимо сделать подробный план помещения. Каждая стена должна быть измерена с использованием рулетки.

Внимание! Очень важно делать измерения на уровне пола, ведь бывают случаи (особенно в старых домах), когда стены немного завалены в одну из сторон. Так как происходит измерение пола, необходимо измерять с максимальным прилеганием к стенам

Вторым этапом является проставление полученных измерений на плане. Лучше всего сразу делать это в метрах, но точность каждого замера должна быть до 1 сантиметра. Это необходимо для того, чтобы при выборе необходимого количества материалов, удалось максимально точно подобрать метраж требуемого материала. Рулонные напольные покрытия продаются в погонных метрах.

Округлять можно только в случае небольшого увеличения, чтобы в случае непредвиденных обстоятельство, было достаточное количество материала.

Как высчитать квадратуру комнаты

Чтобы понять, как узнать общую площадь комнаты, необходимо воспользоваться простой формулой и перемножить показания длины на ширину. Как показано на рисунке длинная стена имеет длину в 7 метров а противоположная только 4. Выходит площадь пола будет равна 28 м2. Именно таким образом и находят квадратуру. Обязательно требуется помнить о небольшом запасе, который потребуется для подгонки и подрезки, причем чем сложнее будет вариант укладки, тем больше потребуется брать запас.

Зачастую комнаты не имеют ровной квадратной или прямоугольной формы.Поэтому, перед тем как узнать площадь комнаты в квадратных метрах, необходимо просто разбить комнату на несколько простых фигур (квадраты и прямоугольники) и после считают общую квадратуру. Так например для комнаты у которой форма буквы Г, достаточно разбить ее на 2 прямоугольника, отдельно посчитать площадь, а потом сложить.

Выглядит это все следующим образом:

• вычисляем квадратуру большого прямоугольника: 5 умножаем на 4,35 и получаем 21,75 квадратных метров;
• теперь по тому же принципу второй: 2,5 на 2,65 и получаем 6,625 квадратов;
• далее суммируем общий результат 6,625 + 21,75 и получаем площадь комнаты в размере 28,375 квадратных метров.

Имея на руках полученный точный результат, можно немного округлить его в большую сторону и учитывать 28,4 квадратных метра.

В том случае, если комната имеет участок со срезанной стеной, как показано на картинке, тогда необходимо нарисовать прямоугольник таким образом, чтобы косая делила его на 2 треугольника. Тогда опять получается помещение по форме буквы Г. Далее можно вычислить площадь, по выше представленному методу.

Необходимо будет найти площадь трех прямоугольников. Недостающий участок – половина маленького прямоугольника. Достаточно будет просто найти его площадь и разделить на 2, после чего прибавить к остальным размерам.

Итак, для примера можно использовать следующие данные:

• большой прямоугольник: 1,75 м *1,93 м = 3,3775 м². Чтобы было проще, возьмем 3,38 м²;
• средний прямоугольник: 1,18 м * 0,57 м = 0,6726 м². Опять произведем округление до 0,67 м²;
• самый маленький прямоугольник: 0,57 м *0,57 м = 0,3249 м2, доводим до 0,33 м²;
• теперь осталось только сложить получившиеся значения и прибавить ½ маленького прямоугольника: 3,38 + 0,67 +0,33/2 = 3,38 + 0,67 +0,17 = 4,22 м².

Это наиболее удобная методика, которой может воспользоваться любой желающий. Достаточно только разбивать сложную фигуру на несколько простых. Несмотря на то, что измерений будет больше, такой метод не требует больших усилий и временных потерь, а все вычисления можно сделать буквально на коленке.

Как посчитать квадратные метры стены с окном

В таком случае надо отдельно высчитать размер стены, отдельно – размер окна. Потом из большей площади вычесть меньшую. Получится число метров квадратных, которое необходимо будет покрыть краской или штукатуркой.

Алгоритм действий:

1. По уже пройденному сценарию высчитать размер стены. Пускай будет уже известное число – 15,4 м2.
2. Далее измерить высоту и длину окна. Перемножить числа. К примеру: длина 1,5 м, высота 1,2 м. Если умножить, то получится 1,8. Значит, площадь окна 1,8 кв. м.
3. Берем площадь стены и вычитаем из нее размер окна: 15,4 – 1,8 = 13,6. Площадь, которую необходимо будет привести в порядок, – 13,6 кв. м.

Площадь комнаты в квадратных метрах

Посчитать несложно, требуется только вспомнить простейшие формулы а также провести измерения. Для этого нужны будут:

• Рулетка. Лучше — с фиксатором, но подойдет и обычная.
• Бумага и карандаш или ручка.
• Калькулятор (или считайте в столбик или в уме).

Набор инструментов нехитрый, найдется в каждом хозяйстве. Проще измерения проводить с помощником, но можно справиться и самостоятельно.

Для начала надо измерить длину стен. Делать это желательно вдоль стен, но если все они заставлены тяжелой мебелью, можно проводить измерения и посередине. Только в этом случае следите чтобы лента рулетки лежала вдоль стен, а не наискосок — погрешность измерений будет меньше.

Прямоугольная комната

Если помещение правильной формы, без выступающих частей, вычислить площадь комнаты просто. Измеряете длину и ширину, записываете на бумажке. Цифры пишите в метрах, после запятой ставите сантиметры. Например, длина 4,35 м (430 см), ширина 3,25 м (325 см).

Как высчитать площадь комнаты

Найденные цифры перемножаем, получаем площадь комнаты в квадратных метрах. Если обратимся к нашему примеру, то получится следующее: 4,35 м * 3,25 м = 14,1375 кв. м. В данной величине оставляют обычно две цифры после запятой, значит округляем. Итого, рассчитанная квадратура комнаты 14,14 квадратных метров.

Помещение неправильной формы

Если надо высчитать площадь комнаты неправильной формы, ее разбивают на простые фигуры — квадраты, прямоугольники, треугольники. Потом измеряют все нужные размеры, производят расчеты по известным формулам (есть в таблице чуть ниже).

Перед тем как посчитать площадь комнаты, тоже проводим изменения. Только в этом случае цифр будет не две, а четыре: добавится еще длина и ширина выступа. Габариты обоих кусков считаются отдельно.

Один из примеров — на фото. Так как и то, и другое — прямоугольник, площадь считается по той же формуле: длину умножаем на ширину. Найденную цифру надо отнять или прибавить к размеру помещения — в зависимости от конфигурации.

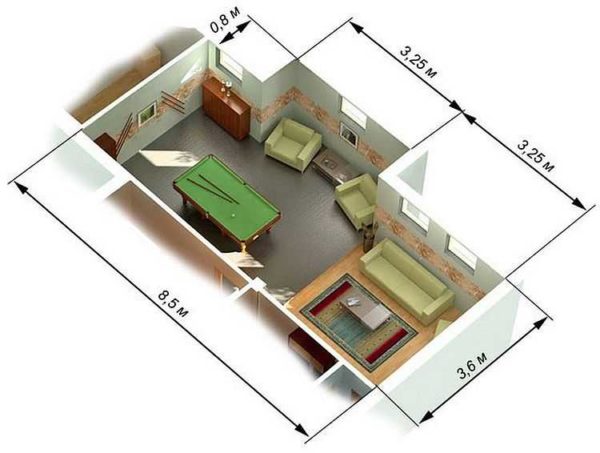
Площадь комнаты сложной формы

Покажем на этом примере как посчитать площадь комнаты с выступом (изображена на фото выше):

1. Считаем квадратуру без выступа: 3,6 м * 8,5 м = 30,6 кв. м.
2. Считаем габариты выступающей части: 3,25 м * 0,8 м = 2,6 кв. м.
3. Складываем две величины: 30,6 кв. м. + 2,6 кв. м. = 33,2 кв. м.

Еще бывают помещения со скошенными стенами. В этом случае разбиваем ее так, чтобы получились прямоугольники и треугольник (как на рисунке ниже). Как видите, для данного случая требуется иметь пять размеров. Разбить можно было по-другому, поставив вертикальную, а не горизонтальную черту

Это не важно. Просто требуется набор простых фигур, а способ их выделения произвольный

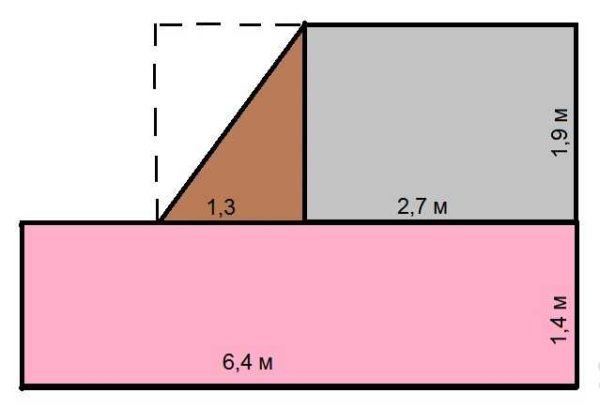
Как посчитать площадь комнаты неправильной формы

В этом случае порядок вычислений такой:

1. Считаем большую прямоугольную часть: 6,4 м * 1,4 м = 8,96 кв. м. Если округлить, получим 9, 0 кв.м.
2. Высчитываем малый прямоугольник: 2,7 м * 1,9 м = 5,13 кв. м. Округляем, получаем 5,1 кв. м.
3. Считаем площадь треугольника. Так как он с прямым углом, то равен половине площади прямоугольника с такими же размерами. (1,3 м * 1,9 м) / 2 = 1,235 кв. м. После округления получаем 1,2 кв. м.
4. Теперь все складываем чтобы найти общую площадь комнаты: 9,0 + 5,1 + 1,2 = 15,3 кв. м.

Планировка помещений может быть очень разнообразной, но общий принцип вы поняли: делим на простые фигуры, измеряем все требуемые размеры, высчитываем квадратуру каждого фрагмента, потом все складываем.

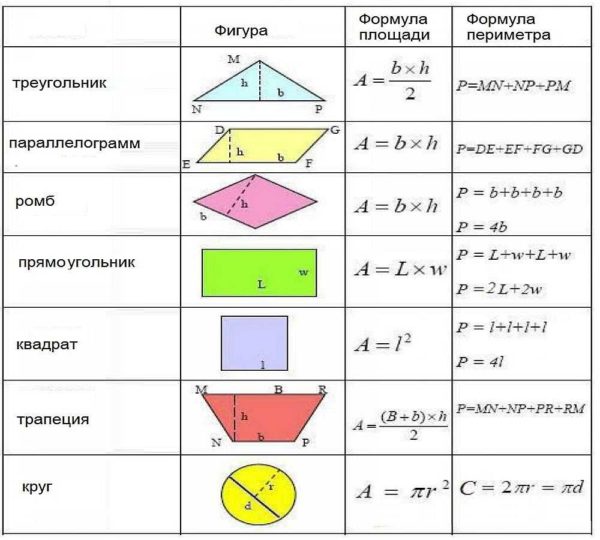
Формулы расчета площади и периметра простых геометрических фигур

Еще одно важное замечание: площадь комнаты, пола и потолка — это все одинаковые величины. Отличия могут быть если есть какие-то полу-колоны, не доходящие до потолка

Тогда из общей квадратуры вычитается квадратура этих элементов. В результате получаем площадь пола.

Методика выполнения работы

Перед тем, как рассчитать квадратуру дома, нужно подготовить следующее:

1. Калькулятор для проведения вычислений. 
2. Рулетка для проведения измерений. При этом надо учитывать, что некоторые производят измерения в дюймах – они не подойдут. Нужна рулетка, которая указывает длину с помощью сантиметров. 
3. Потребуется план квартиры. Измерение площади стен, пола и потолка будет выполняться на его основе. Если такую схему найти нельзя, то её нужно нарисовать от руки, стремясь реалистично отобразить размеры и геометрическую форму частей. 
4. Также потребуется бумага и карандаш для ведения записей в процессе работы. 

При замерах полов, стен и потолков в первую очередь потребуются знания из школьной геометрии. Простейшим способом, как рассчитать площадь дома в квадратных метрах, является вычисление прямоугольных поверхностей. Площадь прямоугольника вычисляется как произведение его сторон. 

Вычисление площади простейших геометрических фигур основано на базовых формулах из геометрииИсточник stroychik.ru

При этом важно учитывать следующее.

Хотя на вид комната состоит из прямоугольных деталей, на самом деле это может оказаться немного по-другому. Например, ширина стен, измеренная с одной и другой стороны, может отличаться на несколько сантиметров. Эта проблема особенно существенна при измерении расстояний в домах старой постройки. В таких случаях обычно измеряют длину в нескольких местах, а при вычислении площади используют среднее значение. 
Вычисления позволяют получить нужные цифры с высокой точностью

Однако будет разумной предосторожностью при вычислениях добавить к площади небольшую величину. Это позволит исключить ситуацию, в которой стройматериалов чуть-чуть не хватило. 

Таким способом можно вычислить площадь прямоугольных пустых стен, пола и потолка.
 

Сложная форма стен и потолка может быть разделена на простые фигуры для упрощения вычисленийИсточник www.buvbaze.lv

Расчёт площади стен с окнами и дверьми

Если на стене есть окно или дверь, то вычисление производится следующим образом:

• Определяется площадь стены без учёта двери или окна. 
• Вычисляется площадь каждого окна или двери путём умножения их длины на ширину. 
• Из площади стены вычитают площадь окон и дверей. 

Этот способ применим в тех случаях, когда рассматриваются прямоугольные стены.

Площадь стены, имеющей неправильную форму

В этом случае нужно разделить вычисления на этапы. Стена с нишами может иметь сложную форму. Однако её всегда можно условно разбить на несколько участков, каждый из которых соответствует одной из простых форм. Затем надо рассчитать площади каждой из частей и сложить их. 

Как посчитать площадь стен, рассказано в видео

Расчёт через периметр

Если комната имеет неправильную форму, то площадь стен можно вычислить, измерив длину периметра. В этом случае проводят измерение горизонтальных отрезков по каждой из сторон помещения и складывают их вместе, затем определяют высоту. Произведение этих величин равно площади стен в этом помещении. 

Несколько советов

• Нужно при проведении расчётов все цифры наносить на план. Таким образом сохранится не только результат, но и промежуточные вычисления, которые могут пригодится при проведении ремонтных работ в будущем. 
• При вычислении площади нужно учитывать, что не всегда необходима полная величина. Например, обои могут клеить не только на всю стену, а на их часть. Класть плитку могут до потолка либо только до определённой высоты. Поэтому нужно точно определить, как высчитать квадратуру дома с учётом конкретного плана ремонта. 

Как сделать замеры – можно посмотреть в видеоролике:

Для того, чтобы точно знать, сколько необходимо стройматериалов для проведения работ, нужно учитывать площади стен, пола и потолка, а также нормы расхода стройматериалов. Среднюю величину расхода можно узнать, спросив у продавцов, а квадратуру дома необходимо измерить самостоятельно. Для этого нужно воспользоваться знаниями из элементарной геометрии. При вычислении площади сложных фигурных поверхностей их разбивают на простые части, делают необходимые вычисления, затем суммируют их. 

Свойство аддитивности площади

Предположим, что нам надо найти площадь прямоугольника со сторонами 2 и 1. Его можно разбить на два квадрата со стороной 1, то есть на два единичных квадрата:

Этот прямоугольник занимает на плоскости в два раза больше места, чем единичный квадрат, поэтому логично считать, что его площадь равна 2. В данном случае мы разбили многоугольник на две фигуры, площадь каждой из которых нам была известна. Далее мы сложили площади известные нам площади и получили площадь прямоугольника.

В общем случае справедливо утверждение, что площадь всякой фигуры равна сумме площадей фигур, из которых она может быть составлена. Это свойство называют аддитивностью площади:

Площадь – не единственная величина, обладающая свойством аддитивности. Например, длина любого отрезка равна сумме длин отрезков, из которых он состоит. В классической физике считается, что масса сложного тела равна сумме масс тел, составляющих его. Аддитивность можно считать основным свойством площади.

Свойство аддитивности подсказывает нам, как измерять площадь произвольных многоугольников. Достаточно разбить такой многоугольник на несколько фигур, чья площадь нам известна, и сложить их площади.

Задание. Найдите площадь фигуры, показанной на рисунке. Длина стороны одной клеточки равна единице.

Решение. Каждая клеточка является, по сути, единичным квадратом, чья площадь равна 1. Можно видеть, что нарисованная фигура состоит 11 таких квадратов:

В силу свойства аддитивности площадь фигуры равна сумме площадей этих квадратов:

Если две фигуры можно разбить на одинаковые фигуры, то их называют равносоставленными фигурами. Покажем пример равносоставленных фигур, которые состоят из двух половинок круга:

Довольно очевидно, что равносоставленные фигуры имеют равную площадь. Также очевидно, что любые две равные фигуры являются равносоставленными, а потому их площади тоже равны.

Важно понимать разницу между равными и равносоставленными фигурами. Фигуры равны, если их можно наложить друг на друга, и при этом они полностью совпадут

Равносоставленные же фигуры могут и не накладываться друг на друга.

Ещё одно важное понятие – равновеликие фигуры. Так называют фигуры, чьи площади равны

Мы уже сказали, что любые две равносоставленные фигуры имеют одинаковую площадь, то есть являются равновеликими. Верно ли обратное? Всякие ли равновеликие фигуры являются равносоставленными? Оказывается, что нет. Можно нарисовать окружность и квадрат, имеющие равные площади, но разбить их на одинаковые фигуры не получится:

С помощью равных и равновеликих фигур можно находить площади фигур, которые невозможно разбить на единичные квадраты.

Задание. Найдите площадь прямоугольного треугольника, катеты которого равны единице.

Решение. Достроим такой прямоугольник до единичного квадрата. В результате гипотенуза треугольника окажется диагональю квадрата:

Получили, что единичный квадрат состоит из двух равных треугольников, чью площадь нам и надо найти. Обозначим площадь треугольника как S. Тогда справедливо равенство

Итак, зная свойства площади фигур, мы попытаемся дать этому понятию определение. Можно сказать, что площадь – это число, характеризующее плоскую фигуру и имеющее следующие свойства:

• площадь квадрата со стороной 1 равна единице:
• равносоставленные фигуры имеют равную площадь.

Такого описания вполне достаточно, чтобы вывести все формулы для нахождения площади многоугольников.

Этапы расчета

Как рассчитать обои? Необходимо прибегнуть к поэтапному выполнению действий, это поможет учесть все нюансы и получить точный результат. Многие считают, что определить, сколько обоев нужно, просто. Но в итоге упущенными оказываются важные факторы, что приводит к довольно неприятным последствиям.

Определение параметров различных обоев

Сразу стоит оговориться, что без выбора конкретного вида материала подсчет будет условным. Поэтому работы начинаются с определения стандартных параметров всех имеющихся разновидностей, из которых будет сделан окончательный выбор.

Итак, существуют следующие размеры:

1. Самым популярным считается параметр шириной 53 см и длиной 10,05 м. С таким материалом удобно работать без наличия специальных навыков. Единственная возникающая трудность – это подгонка и многочисленные швы.
2. Разновидность с шириной более одного метра, а точнее, 106 см. При этом стандартная длина также составляет 1005 см. Но встречаются варианты с разбегом от 15 до 25 метров. Необходимо учитывать, что такие полотна имеют большую плотность, это сказывается на их весе. Соответственно, облицовывать поверхности становится значительно сложнее, хотя уменьшается количество стыков.
3. Нестандартными вариантами считаются материалы, имеющие ширину 60, 68, 74 и 138 см. В большинстве случаев это специальные изделия или изготовленные за рубежом.

Подгонка полотна

Может показаться, что зная все параметры, можно точно определить расход обоев. Но довольно сложно представить ситуацию, когда все полосы накладываются на поверхность с абсолютной точностью. В действительности, существует ряд факторов, влияющих на правильность подсчета:

• Технология раскроя предполагает, что при нарезке полотен обязательно оставляют припуск, который может составлять до 5 см. В большинстве случаев это даже не связано с соблюдением технологии, просто практически все стены имеют перекос. Для вычисления отклонений можно проводить промеры, но это значительно усложнит и замедлит работу. К тому же ошибки будут неизбежны.
• Также нельзя забывать о том, что часто при наличии рисунка требуется совмещение смежных элементов, иногда сдвиг может достигать половины полосы. Таким образом, чтобы понять, сколько надо обоев на конкретную стену, следует ознакомиться со схемой наклейки, которую предлагает каждый производитель. Но зачастую она имеет лишь условные обозначения.
• Конечно, нельзя игнорировать особенности помещения и серьезные перепады высоты потолка. Этот показатель может составлять 70–90 см и более. Таким значительным отклонением обладают чердачные комнаты, имеющие пологий скос потолка.

Все стадии подсчета учитываются в обязательном порядке, это помогает избежать досадных и нелепых ошибок.

На стандартной маркировке есть несколько обозначений связанных с подгонкой рисунка, они напрямую касаются количества рулонов

Возникает закономерный вопрос: зачем точно определять, сколько обоев нужно на комнату? Действительно, если приобретать материал с достаточным запасом, то абсолютно точные параметры не нужны, но бывают ситуации, когда в работе используются дорогие изделия или финансовые возможности ограничены.

Существует масса оттенков цветового спектра и не стоит рассчитывать, что в другой партии обоев палитра совпадет на 100 %

Определение параметров помещения

Чтобы рассчитать необходимое количество обоев, нужно определить основные параметры помещения.

1. Все начинается с замера периметра с помощью подручного измерительного прибора. Как известно, для получения этого показателя складывается длина всех сторон помещения. К примеру, прямоугольная комната имеет четыре стены размером 405, 506, 403 и 505 см, в этом случае периметр составит 1819 см. Следует учитывать, что одинаковых стен практически не бывает.
2. Некоторые трудности могут возникать с дверными и оконными проемами. Их можно не учитывать, если в итоге получается большой запас. Но рекомендуется замерить все участки, расположенные над и под проемами, чтобы включить их отдельно.
3. Высота потолков. Сразу определяется, как будет располагаться облицовочный материал. Часто случается, что полотна занимают только часть поверхности или комбинируются. Поэтому чтобы узнать, сколько нужно рулонов, берется конкретная высота с учетом особенностей помещения.
4. Площадь. Этот показатель помогает рассчитать, сколько понадобится материала в квадратных метрах. Чтобы получить необходимое число, длину умножают на высоту.

Основываясь на имеющихся параметрах, удается рассчитать обои на комнату с наибольшей точностью.

Помещение с косыми стенами

Существуют и такие помещения, форма которых походит на сложный многоугольник. К тому же, в такой комнате не все углы могут быть прямыми (т.е., иметь 90 о), что еще более усложняет задачу. Как должен производиться расчёт потолка в таком случае?

Если речь идет о периметре потолка, то здесь всё просто. Нужно, с помощью рулетки, всего-навсего измерить общую длину всех стен (отрезков) в комнате.

Для вычисления площади такого потолка, вначале нужно произвести те же действия, что и в предыдущем случае: то есть, начертить эскиз комнаты и снять все необходимые замеры. Затем нужно внимательно изучить эскиз и «раскроить» его так, чтобы в конечном итоге получить только правильные геометрические фигуры — прямоугольники и прямоугольные треугольники.

После этого можно начинать расчёт площади потолка. Для этого нужно вспомнить из школьного курса геометрии формулу вычисления площади для прямоугольного треугольника. Напомним, что площадь этой фигуры — это произведение двух катетов треугольника, разделенное пополам (катеты — это те стороны треугольника, которые примыкают непосредственно к его прямому углу). Например, если на вашем эскизе длина катетов образованного треугольника составляет 1,2 и 0,8 м, то расчёт его площади будет иметь такой вид: 1,2 х 0,8 / 2 = 0,48 м 2 .

Как посчитать площадь: вспоминаем основные формулы

Многих интересует, как узнать площадь конкретного помещения, зная его линейные размеры. На первый взгляд расчет может показаться слишком трудоемким. Многие предпочитают обращаться за помощью к специалистам, полагая, что в этом случае удастся избежать ошибок. Если же не хочется платить деньги за работу, которую без труда можно выполнить самостоятельно, стоит вспомнить основные формулы расчета площади. С их помощью можно будет подсчитать квадратуру любого помещения.

Вспоминаем основные формулы

Каждый без труда ответит, как рассчитать площадь прямоугольной или квадратной поверхность. Треугольная, круглая или в форме сегмента способна вызвать определенные трудности. Обновив знания, можно будет сразу приступать к расчетам площади помещения простой формы.

Зная порядок расчета простых, несложно понять, как вычислить площадь сложной поверхности. Даже самую замысловатую фигуру можно разбить на множество простых, а затем, выполнив расчет каждой, найти суммарное значение.

Сложную фигуру разбиваем на простые

Как посчитать площадь треугольника: используем проверенные формулы

Треугольное помещение встречается редко. Однако если комната имеет нестандартную планировку, ее мысленно разделяют на простые фигуры, одной из которых и может быть треугольник. Как вычисляется площадь треугольника? Достаточно просто. Все расчеты можно выполнить самостоятельно или с помощью онлайн калькулятора.

Чтобы посчитать площадь треугольника своими силами, лучше воспользоваться следующей формулой:

S = 1/2 × Н × А, где

А – сторона;

Н – высота, проведенная к этой высоте. Численно равна длине перпендикуляра, опущенного из угла, противоположного данной стороне.

Квадратуру треугольника можно найти по-разному

Вычисление по данной формуле достаточно прост. Однако если в процессе снятия размеров будет допущена ошибка, например, из-за неправильного измерения высоты, полученное значение может значительно отличаться от истинного. Чтобы этого избежать, можно использовать более сложную формулу Герона, позволяющую найти квадратуру треугольника по длинам трех его сторон: А, В и С.

Для вычисления потребуется найти полупериметр р, численно равный ½(А+В+С). Площадь треугольника в этом случае будет равна квадратному корню из произведения р × (р — А) × (р — В) × (р — С).

Формула Герона поможет найти искомую площадь

Онлайн калькуляторы предлагают воспользоваться сразу несколькими методиками расчета по:

• Основанию и проведенному к нему основанию;
• Формуле Герона;
• Длинам смежных сторон и углу между ними.

Покрытие пола

Для покупки половых покрытий тоже важно знать, как посчитать периметр комнаты. Формула все та же: сумма длин всех сторон

При этом нет необходимости обращать внимание на двери и окна. Достаточно либо измерить две смежные стороны и умножить на два, либо измерить каждую сторону комнаты и сложить эти цифры

Рассчитать покрытие для пола, зная периметр и длины, будет совсем не сложно. Зачастую на сайтах, продающих эти самые покрытия, имеются специальные калькуляторы. В них необходимо ввести длину и ширину комнаты, желаемое покрытие. После этого появится информация о том, сколько материала необходимо приобретать. Если речь идет о линолеуме, то варианты его ширин соответствуют стандартным торцевым сторонам комнаты. Поэтому покупают его, исходя из длины комнаты.

Если покупать кафель, паркет или ламинат, необходимы более сложные расчеты. Вероятно, для этого лучше воспользоваться помощью менеджеров, работающих в строительном магазине или торговой точке, где вы будете покупать покрытие.

Периметр прямоугольника

Прямоугольник — это четырехугольник, у которого все четыре угла прямые, то есть, составляют 90 градусов. Частным случаем прямоугольника могут быть квадрат или ромб.

Периметр прямоугольника — это сумма длин всех его ребер.

Основные свойства прямоугольника:

• противоположные стороны фигуры равны и параллельны друг другу;
• сумма всех углов равна 360 градусов;
• диагонали прямоугольника равны по длине и точкой пересечения делятся пополам;
• диагонали делят фигуру на два одинаковых прямоугольных треугольника;
• по теореме Пифагора, квадрат диагонали прямоугольника равен сумме квадратов двух его соседних ребер;
• стороны рассматриваемого четырехугольника также являются его высотами;
• точка пересечения диагоналей — это центр прямоугольника и также центр вписанной окружности;
• диагональ этого четырехугольника — это диаметр описанной окружности;
• вокруг него всегда можно описать окружность.