Что такое развертка конуса и как ее построить? формулы и пример решения задачи

Какими могут быть поделки из конусов?

Собака

Скрутите половинку круга из коричневой бумаги в конус – туловище готово. Добавьте собачьи ушки, мордочку, лапы и глаза и получится симпатичный песик, а главное – совсем простой в создании.

Слон

Основа, то есть туловище слона – серый тонкий конус из четвертой части круга. Плюс голова с большими ушами, плавно перетекающая в хобот, ноги и хвост. Все просто и быстро, тем более что в помощь прилагается шаблон головы.

Простой бумажный кот

Простейшая поделка, состоит из черного конуса и цилиндрической небольшой головы, прикрепленной на вершине конуса. также понадобятся торчащие ушки, удлиненные глаза, нос, усы, лапы и хвост. Коты в этой технике смотрятся оригинально, красивы в различных расцветках.

Лев

Работа интересна не только конусным туловищем, но и головой, грива вокруг которой из тонких бумажных полосок, склеенных в петли. Часто таким способом мастерят цветы.

Ворона

Из конуса можно сделать забавную ворону или вороненка. Причем работа очень простая. Основа – черный конус, крылья единым целым и голова в виде круга. А также понадобится из желтой бумаги широкий клюв и лапы в виде полос бумаги, сложенных в гармошку.

Бумажные пингвины

Работа настолько простая, что за считанные минуты можно сделать целое семейство пингвинов, с мамой, папой и малышами. Дети быстро запоминают последовательность действий и с легкостью справляются с заданием.

Дракон Беззубик

В продолжении черных персонажей, представляю вам симпатягу Беззубика из мультфильма «Как приручить дракона». Он также состоит из конусного туловища и дополняющих бумажных частей, для создания которых в помощь есть шаблон.

Лягушка

Отличная поделка из конуса, максимально простая. Туловище – широкий зеленый конус, плюс минимум дополняющих деталей в виде четырех одинаковых лап, глаз и языка. Все.

Яркие бабочки

Поделка очень похожа на предыдущую, отличается только формой крыльев и расцветками. Такую бабочку предельно легко сделать, главное — наличие цветной бумаги различных оттенков и собственная фантазия.

Свинка из конуса

Простейшая поделка для детей, даже самых маленьких. Возможно, им понадобится небольшая помощь в создании конуса, а с остальными составляющими они справятся с удовольствием и без проблем.

Конусные курочки

Здесь конус не в оригинальном своем виде, так как при его свертывании нужно оставить кончики. Но все равно техника одинаковая, курочки сделать легко, как и все поделки из конусов.

Божья коровка

Скорее всего, это кулек-сюрприз в виде божьей коровки, с который можно положить сладости и презентовать такой подарок маме. Беря за основу конус, можно сделать такой сюрприз в виде самых разных персонажей.

Поэтапный инструктаж смотрите .

Ведьмочка

Из конуса можно сделать не только животных. В данном варианте – это ведьма, но также это могут быть любые человечки, сказочные персонажи, например, звездочет, лесные феи, гномы, и даже снеговик.

Ежик

Посмотрите, какого можно сделать замечательного ежика! Причем еж полностью состоит из конусов, только некоторые из них разрезанные, чтобы получилось подобие иголок. И сам он не в вертикальном положении, как предыдущие поделки из конусов, а горизонтальном.

Для новогоднего оформления квартиры очень хорошо подходят маленькие ёлочки из подручных материалов. Один из главных плюсов таких ёлочек – простота изготовления и широкое поле для фантазии при их украшении. Кроме того, таких ёлочек можно сделать сразу много – разных по виду и украшению и расставить по всей квартире, таким образом, оригинально украсив её. Проще всего сделать ёлочку-конус из бумаги. На специализированных сайтах есть множество идей украшения таких ёлок, к которым Вы всегда сможете добавить свою авторскую выдумку. При всём разнообразии моделей, основа у всех ёлочек одна – конус из бумаги или картона.

Круглый прямой конус

В общем случае конусом является фигура, построенная в результате движения отрезка вдоль некоторой кривой на плоскости, при этом второй конец отрезка зафиксирован в определенной точке пространства. Сам отрезок называется генератрисой, или образующей, а кривая — директрисой, или направляющей.

Согласно приведенному определению, кривая, которая ограничивает фигуру, может быть совершенно любого типа. Самыми известными из них являются парабола, гипербола, эллипс и окружность. В последнем случае говорят о круглом конусе.

Круглый конус может быть наклонным и прямым. Обе фигуры показаны ниже на рисунке.

Здесь r — радиус окружности, которая ограничивает основание фигуры. Буквой h обозначена высота, которая представляет опущенный на основание из вершины конуса перпендикуляр. Буквой a обозначена ось конуса. Видно, что в случае прямой фигуры его высота совпадает с осью, то есть пересекает окружность в ее центре.

Помимо радиуса r и высоты h, важным линейным параметром конуса является длина его образующей g. Как было сказано, образующая — это отрезок, соединяющий директрису с высотой. Для прямого круглого конуса все образующие равны друг другу.

Далее в статье, раскрывая вопрос касательно того, как найти диаметр конуса, будет рассматриваться только конус круглый и прямой.

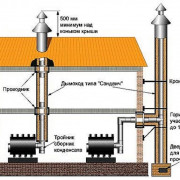
Колпак на дымоход своими руками

Хозяева домов зачастую прибегают к использованию элементов в виде различных колпаков и зонтов, служащих, как это кажется на первый взгляд, для украшения дымовых труб. В то же время такие насадки не только улучшают эстетическое восприятие строения, но и обеспечивают полезную функциональность. Обычно так называемый козырек для дымохода изготавливается собственными силами, так как для этого не требуется серьезных знаний и умений. Хотя наряду с простой конструкцией этих элементов встречаются достаточно замысловатые поделки, которые проблематично соорудить без соответствующего опыта.

Конструктивные особенности

Колпак на дымоход представляет собой устройство, предназначенное для защиты трубы от попадания влаги. Внешний вид таких козырьков может быть различен, что имеет зависимость как от предпочтений хозяина дома, так и от конфигурации трубы.

Колпаки на трубу дымохода включают в себя:

• зонтик – устанавливаемая на вершине колпака защита от осадков, посторонних предметов и проникновения птиц, внешний вид которой имеет форму пирамиды, конуса или соответствует другой геометрии;
• фартук – часть колпака, отвечающая за защиту верха трубы от стекающей с зонтика воды. Обычно установка этого элемента производится при оснащении прямоугольной или квадратной трубы. В результате гарантируется увеличение срока службы дымохода, так как удается практически исключить вероятность появления коррозии и грибка;
• кронштейны – крепежные элементы, представляющие собой металлические полоски, которые позволяют соединить козырек и фартук. Непосредственное крепление в данном случае производится за счет использования сварки.

Имейте в виду! Собрать колпак для дымохода вполне реально самому, но только в том случае, если вы хотите установить достаточно простой флюгарок. Модели, отличающиеся большей сложностью в плане конструктивных особенностей, гораздо выгоднее заказать или купить.

При наличии выбора лучше всего отдать предпочтение тем моделям, которые оборудованы открывающейся крышкой. Это позволит проводить профилактический осмотр дымохода и его чистку без каких-либо проблем, что связано с комфортом доступа.

Колпак на дымоход долгого срока использования может быть изготовлен только из железа, устойчивого к коррозии: оцинкованная сталь, алюминий и медь. В последнем случае предлагаемый металл обладает ярко выраженным декоративным характером, так как его переливы на солнце могут придать вашем дому определенную респектабельность.

Одевают оголовок на трубу дымохода чтобы гасить искры. Это одно из его предназначений. Поэтому качество железа должно быть хорошим, тем самым оно долго не прогорит.

Виды

В связи с тем, что дымоходы отличаются разнообразием форм и размеров, производители колпаков также предлагают широкий ассортимент продукции. Если вы решите украсить свое жилище и продлить срок жизни дымохода, то придется выбирать среди большого ассортимента флюгарок:

1. Стандартные – зонт на дымоход в виде пирамидки, для изготовления которой используется листовой металл, а крепление к фартуку осуществляется посредством кронштейнов.
2. Четырехскатные – устанавливается преимущественно на прямоугольные трубы, выполненные из кирпича. По форме соотносится с вальмовой крышей с четырьмя скатами.
3. С полукруглым зонтиком – визуально отличается красотой, но обеспечивает недостаточную тягу. Преимущественно используется для установки на дымоходах домов, которые построены по европейским стандартам.
4. Плоские – часто можно встретить на зданиях в стиле модерн. Имеет прямоугольную форму и отличается таким недостатком, как повышенная нагрузка на кронштейны, что в некоторых случаях приводит к их деформации. Это связано с плоской крышей колпака, которая не дает возможность скатываться снегу. Данный факт определяет возникновение упомянутой проблемы.
5. Круглые с конусообразным зонтиком – модели без капельника, устанавливаемые на выполненные из нержавейки дымоходы круглого сечения.

Задача на определение диаметра через известную площадь конуса и его образующую

Дан конус, площадь поверхности которого составляет 150 см 2 . Генератриса равна 14 см. Чему равен диаметр конуса?

Для получения ответа на поставленный вопрос используем описанную в статье методику. Сначала выпишем соответствующее уравнение:

r 2 + 14*r — 150/3,14 = 0

При получении последнего равенства мы разделили левую и правую его части на число Пи. Рассчитываем дискриминант D. Имеем:

D = 14 2 — 4*1*(-150/3,14) = 387,0828

Полученный дискриминант приведен с точностью до 0,0001. Формула для корней уравнения r имеет следующий вид:

Очевидно, что один из корней будет отрицательным. Его не будем вычислять. Определим лишь искомый положительный радиус фигуры:

r = (-14+√387,0828)/2 = 2,837 см

Чтобы найти диаметр конуса, остается умножить это значение на два и записать ответ: d = 5,674 см.

В конце отметим, что, зная два любых параметра круглого конуса прямого, можно определить любую его характеристику, включая объем и площадь поверхности.

Нормальные углы и конусы инструментов

НОРМАЛЬНЫЕ УГЛЫ ( ГОСТ 8908-81 )

&nbsp Таблица не распространяется на угловые размеры конусов. При выборе углов 1-й ряд следует предпочитать 2-му, а 2-й — 3-му.

НОРМАЛЬНЫЕ КОНУСНОСТИ и УГЛЫ КОНУСОВ ( ГОСТ 8593-81 )

&nbsp Стандарт распространяется на конусности и углы конусов гладких конических элементов деталей.

&nbsp Примечание. Значения конусности или угла конуса, указанные в графе «Обозначение конуса», приняты за исходные при расчете других значений, приведенных в таблице. При выборе конусностей или углов конусов ряд 1 следует предпочитать ряду 2.

КОНУСЫ ИНСТРУМЕНТОВ УКОРОЧЕННЫЕ ( ГОСТ 9953-82 )

&nbsp Стандарт распространяется на укороченные инструментальные конусы Морзе.

&nbsp *z — наибольшее допускаемое отклонение положения основной плоскости, в которой находится диаметр D от теоретическогот положения. &nbsp ** размеры для справок.

КОНУСНОСТЬ НАРУЖНЫХ И ВНУТРЕННИХ КОНУСОВ И КОНУСОВ С РЕЗЬБОВЫМ ОТВЕРСТИЕМ

РЕКОМЕНДУЕМЫЕ РАЗМЕРЫ ЦЕНТРОВОГО ОТВЕРСТИЯ УКОРОЧЕННОГО КОНУСА

КОНУСЫ ИНСТРУМЕНТАЛЬНЫЕ МОРЗЕ И МЕТРИЧЕСКИЕ НАРУЖНЫЕ( ГОСТ 25557-2006 )

&nbsp Профиль резьбового отверстия соответствует отверстию центровому форма Р по ГОСТ ГОСТ 14034-74.

&nbsp В ГОСТ 25557-2006 все размеры центрового отверстия приводятся в общей таблице. Стандарт также определяет размеры пазов канавок и отвестий, необходимых для конструирования конусов, в случае подачи смазочно-охлаждающей жидкости (СОЖ) через инструмент.

&nbsp В зависимости от конструкции инструментальный хвостовик может иметь соответствующее обозначение:

BI — внутренний конус с пазом; BE — наружный конус с лапкой; AI — внутренний конус с отверстием по оси; АЕ — наружный конус с резьбовым отверстием по оси; BIK — внутренний конус с пазом и отверстием для подачи СОЖ; ВЕК — наружный конус с лапкой и отверстием для подачи СОЖ; AIK — внутренний конус с отверстием по оси и отверстием для подачи СОЖ; АЕК — наружный конус с резьбовым отверстием по оси и отверстием для подачи СОЖ.

КОНУСЫ ИНСТРУМЕНТАЛЬНЫЕ МОРЗЕ И МЕТРИЧЕСКИЕ ВНУТРЕННИЕ( ГОСТ 25557-2006 )

КОНУСЫ ВНУТРЕННИЕ И НАРУЖНЫЕ КОНУСНОСТЬЮ 7 : 24 ( ГОСТ 15945-82 )

&nbsp Допуски конусов внутренних и наружных конусностью 7:24 по ГОСТ 19860-93.

КОНУСЫ ИНСТРУМЕНТОВ Предельные отклонения угла конуса и допуски формы конусов ( ГОСТ 2848-75 )

&nbsp Степень точности инструментальных конусов обозначается допуском угла конуса заданной степени точности по ГОСТ 8908-81 и определяется предельными отклонениями угла конуса и допусками формы поверхности конуса, числовые значения которых указаны ниже.

&nbsp Примечания: &nbsp 1. Отклонения угла конуса от номинального размера располагав в «плюс» — для наружных конусов, в «минус» — для внутренних. &nbsp 2. ГОСТ 2848-75 для наружных конусов предусматривает также степени точности АТ4 и АТ5. Допуски по ГОСТ 2848-75 распространяются на конусы инструментов по ГОСТ 25557-2006 и ГОСТ 9953-82.

&nbsp Пример обозначения конуса Морзе 3, степени точности АТ8:

Морзе 3 АТ8 ГОСТ 25557-2006

&nbsp То же метрического конуса 160, степени точности АТ7:

Метр. 160 АТ7 ГОСТ 25557-2006

&nbsp То же укороченного конуса В18, степени точности АТ6:

Морзе В18 АТ6 ГОСТ 9953-82

ГОСТ 2848-75 — Конусы инструментов. Допуски. Методы и средства контроля ГОСТ 7343-72 — Конусы инструментов с конусностью 1:10 и 1:7. Размеры ГОСТ 10079-71 — Развертки конические с коническим хвостовиком под конусы Морзе. Конструкция и размеры ГОСТ 22774-77 — Конусы и трубки шлифовальные. Типы и размеры ГОСТ 25548-82 — Основные нормы взаимозаменяемости. Конусы и конические соединения. Термины и определения

Как сделать конус из картона

Вы узнали, как сделать конус из простой бумаги А4, но, если вам нужна плотная поделка, лучше воспользоваться картоном. Материалы и инструменты остаются теми же, что и в предыдущих поделках. Различие заключается только в оттенке картона, его подбираем исходя из предназначения.

Будущий конус будет достаточно прочным за счет чего, его применение может быть широким. Подобную методику работы мы уже рассмотрели выше, но это изготовление все же отличается.

1. Возьмите картон нужного оттенка. Определите середину листа и используя циркуль начертите круг.
2. Полученную окружность нужно разделить на четыре равные доли. Для разделения фигуры на правильные части проведите через полученную ранее точку в центре прямые линии.
3. Складываем круг в разных направлениях. Вы получите четыре сегмента. Один из них нужно вырезать.
4. Полученную заготовку сворачиваем образуя колпак. Так как картон может не сразу склеиться, закрепляем низ фигуры степлером. И только затем промазываем фигуру ПВА.

Плотный конус готов. Если вам нужна не одна геометрическая фигура, а несколько, первый полученный круг, в котором уже вырезана одна четверть, можно использовать в качестве шаблона.

Как построить развертку поверхности прямого усеченного конуса

Делим основание конуса на 12 равных частей (вписываем правильную пирамиду). Данные элементы построения уже готовы из чертежа «Сечение конуса плоскостью частного положения».

Строим развертку боковой поверхности конуса, которая представляет собой круговой сектор. Центр его радиуса принимается за вершину конуса, а величина радиуса кругового сектора конуса равна длине образующей конуса, а длина дуги сектора равна длине окружности основания конуса. На дугу сектора переносим 12 хорд, которые определят ее длину, а также угол кругового сектора.

К центральной точке дуги сектора боковой развертки усеченного конуса пристраиваем основание конуса. Его основание проецируется в натуральную величину на горизонтальную плоскость проекции.

На развертке конуса к его основанию пристраиваем натуральную величину сечения.

Две крайние образующие конуса, которые формируют его основной контур, проецируются на фронтальную плоскость проекции в натуральную величину, поэтому их можно сразу переносить на развертку боковой поверхности конуса. Так как часть его срезана фронтально проецирующей плоскостью, то перенесем на развертку конуса только крайнюю правую усеченную образующую.  Остальные усеченные образующие конуса проецируются на фронтальную плоскость проекций с искажением. Их натуральную величину находят способом вращения вокруг оси конуса до положения, параллельного фронтальной плоскости проекций.

Сам принцип нахождения натуральных величин образующих усеченного конуса сводится к тому, что проводят из точек пересечения образующих с плоскостью горизонтальную прямую до крайней правой (левой) образующей и на ней отмеряют натуральные их величины. Все действия проводят на фронтальной плоскости проекции.

На каждой образующей, лежащей на развертке боковой поверхности конуса, откладываем действительные длины усеченных образующих. Полученные точки соединяем плавной кривой линией команда Сплайн в Автокад.

Мы выполнили задачу начертательной геометрии на построение развертки усеченного конуса, но чтобы не возникло проблем во время ее защиты (когда я обучался, каждая курсовая по начертательной геометрии защищалась), еще раз рассмотрим принцип вращения для нахождения натуральной величины усеченной образующей конуса.

«Их натуральную величину находят способом вращения вокруг оси конуса до положения, параллельного фронтальной плоскости проекций.» Когда мы вращаем образующую прямого конуса до положения параллельного фронтальной плоскости проекции, то ее траектория описывает дугу на горизонтальной плоскости проекции, а на фронтальной прямую!

Вы можете не проводить линии связи с горизонтальной плоскости проекции на фронтальную, ведь очевидно, что точка будет лежать на крайней основной образующей контура конуса для каждой образующей при нахождении ее натуральной величины. Поэтому сам принцип вращения по нахождению натуральной величины образующих конуса сводится к проведению из точек усеченных образующих горизонтальной прямой до основной образующей контура конуса.

В видеоуроке очень наглядно и подробно показан принцип построения развертки прямого усеченного конуса.

Выкройка для конуса

19.11.2012 // Владимир Трунов

Вместо слова «выкройка» иногда употребляют «развертка», однако этот термин неоднозначен: например, разверткой называют инструмент для увеличения диаметра отверстия, и в электронной технике существует понятие развертки. Поэтому, хоть я и обязан употребить слова «развертка конуса», чтобы поисковики и по ним находили эту статью, но пользоваться буду словом «выкройка».

Построение выкройки для конуса — дело нехитрое. Рассмотрим два случая: для полного конуса и для усеченного. На картинке (кликните, чтобы увеличить) показаны эскизы таких конусов и их выкроек. (Сразу замечу, что речь здесь пойдет только о прямых конусах с круглым основанием. Конусы с овальным основанием и наклонные конусы рассмотрим в следующих статьях).

Полный конус

Обозначения:

• — диаметр основания конуса;
• — высота конуса;
• — радиус дуги выкройки;
• — центральный угол выкройки.

Параметры выкройки рассчитываются по формулам: ; ; где .

Усеченный конус

Обозначения:

• — диаметр большего основания конуса;
• — диаметр меньшего основания конуса;
• — высота конуса;
• — радиус внешней дуги выкройки;
• — радиус внутренней дуги выкройки;
• — центральный угол выкройки.

Формулы для вычисления параметров выкройки: ; ; ; где . Заметим, что эти формулы подойдут и для полного конуса, если мы подставим в них .

Угол при вершине конуса

Иногда при построении конуса принципиальным является значение угла при его вершине (или при мнимой вершине, если конус усеченный). Самый простой пример — когда нужно, чтобы один конус плотно входил в другой. Обозначим этот угол буквой (см. картинку). В этом случае мы можем его использовать вместо одного из трех входных значений: , или . Почему «вместо«, а не «вместе«? Потому что для построения конуса достаточно трех параметров, а значение четвертого вычисляется через значения трех остальных. Почему именно трех, а не двух и не четырех — вопрос, выходящий за рамки этой статьи. Таинственный голос мне подсказывает, что это как-то связано с трехмерностью объекта «конус». (Сравните с двумя исходными параметрами двухмерного объекта «сегмент круга», по которым мы вычисляли все остальные его параметры в статье Геометрия круга.)

Ниже приведены формулы, по которым определяется четвертый параметр конуса, когда заданы три.

• Заданы ; тогда .
• Заданы ; тогда .
• Заданы ; тогда .
• Заданы ; тогда .

Методы построения выкройки

• Вычислить значения на калькуляторе и построить выкройку на бумаге (или сразу на металле) при помощи циркуля, линейки и транспортира.
• Занести формулы и исходные данные в электронную таблицу (например, Microsoft Exel). Полученный результат использовать для построения выкройки при помощи графического редактора (например, CorelDRAW).
• использовать мою программу Cones, которая нарисует на экране и выведет на печать выкройку для конуса с заданными параметрами. Эту выкройку можно сохранить в виде векторного файла и импортировать в CorelDRAW.

Не параллельные основания

Что касается усеченных конусов, то программа Cones пока строит выкройки для конусов, имеющих только параллельные основания. Для тех, кто ищет способ построения выкройки усеченного конуса с не параллельными основаниями, привожу ссылку, предоставленную одним из посетителей сайта:

Усеченный конус с не параллельными основаниями.

tvlad.ru

Что такое уклон? Как определить уклон? Как построить уклон? Обозначение уклона на чертежах по ГОСТ.

Уклон. Уклон это отклонение прямой линии от вертикального или горизонтального положения. Определение уклона. Уклон определяется как отношение противолежащего катета угла прямоугольного треугольника к прилежащему катету, то есть он выражается тангенсом угла а. Уклон можно посчитать по формуле i=AC/AB=tga.

Читать также: Сабельная пила для газоблока

Построение уклона. На примере (рисунок ) наглядно продемонстрировано построение уклона. Для построения уклона 1:1, например, нужно на сторонах прямого угла отложить произвольные, но равные отрезки. Такой уклон, будет соответствовать углу в 45 градусов. Для того чтобы построить уклон 1:2, нужно по горизонтали отложить отрезок равный по значению двум отрезкам отложенным по вертикали. Как видно из чертежа, уклон есть отношение катета противолежащего к катету прилежащему, т. е. он выражается тангенсом угла а.

Обозначение уклона на чертежах. Обозначение уклонов на чертеже выполняется в соответствии с ГОСТ 2.307—68. На чертеже указывают величину уклона с помощью линии-выноски. На полке линии-выноски наносят знак и величину уклона. Знак уклона должен соответствовать уклону определяемой линии, то есть одна из прямых знака уклона должна быть горизонтальна, а другая должна быть наклонена в ту же сторону, что и определяемая линия уклона. Угол уклона линии знака примерно 30°.

Технология нарезания внутренней резьбы

Как уже говорилось выше, перед началом работы надо просверлить отверстие, диаметр которого должен точно подходить под резьбу определенного размера. Следует иметь в виду: если диаметры отверстий, предназначенных под нарезание метрической резьбы, выбраны неверно, это может привести не только к ее некачественному выполнению, но и к поломке метчика.

Учитывая тот факт, что метчик, формируя резьбовые канавки, не только срезает металл, но и продавливает его, диаметр сверла для выполнения резьбы должен быть несколько меньше, чем ее номинальный диаметр. Например, сверло под выполнение резьбы М3 должно иметь диаметр 2,5 мм, под М4 – 3,3 мм, для М5 следует выбирать сверло диаметром 4,2 мм, под резьбу М6 – 5 мм, М8 – 6,7 мм, М10 – 8,5 мм, а для М12 – 10,2.

Таблица 1. Основные диаметры отверстий под метрическую резьбу

Все диаметры сверл под резьбу ГОСТ приводит в специальных таблицах. В таких таблицах указаны диаметры сверл под выполнение резьбы как со стандартным, так и с уменьшенным шагом, при этом следует иметь в виду, что для этих целей сверлятся отверстия разных диаметров. Кроме того, если резьба нарезается в изделиях из хрупких металлов (таких, например, как чугун), диаметр сверла под резьбу, полученный из таблицы, необходимо уменьшить на одну десятую миллиметра.

Диаметры сверл под метрическую резьбу можно рассчитать самостоятельно. От диаметра резьбы, которую требуется нарезать, необходимо вычесть значение ее шага. Сам шаг резьбы, размер которого используется при выполнении таких вычислений, можно узнать из специальных таблиц соответствия. Для того чтобы определить, какого диаметра отверстие необходимо выполнить с помощью сверла в том случае, если для резьбонарезания будет использоваться трехзаходный метчик, надо воспользоваться следующей формулой:

Д о = Д м х 0,8,

где:

Д о

– это диаметр отверстия, которое надо выполнить с помощью сверла,

Д м

– диаметр метчика, которым будет обрабатываться просверленный элемент.

Казалось бы что в трубах сложного? Соединяй и крути… Но, если вы не сантехник и не инженер с профильным образованием, то обязательно возникнут вопросы за ответами на которые придется идти куда глаза глядят. А глядят они скорее всего первым делом в интернет)

Ранее мы уже говорили о диаметрах металлических труб в этом материале . Сегодня же попробуем внести ясность в резьбовые соединения труб различного назначения. Мы постарались не загромождать статью определениями. Базовую терминологию содержит ГОСТ 11708-82

с которым каждый может ознакомиться самостоятельно.

Формула для определения конусности

Провести самостоятельно расчет конусности можно при применении различных формул. Стоит учитывать, что в большинстве случаев показатель указывается в градусах, но может и в процентах – все зависит от конкретного случая. Алгоритм проведения расчетов выглядит следующим образом:

1. K=D-d/l=2tgf=2i. Данная формула характеризуется тем, что конусность характеризуется двойным уклоном. Она основана на получении значения большого и меньшего диаметра, а также расстояния между ними. Кроме этого определяется угол.
2. Tgf=D/2L. В данном случае требуется протяженность отрезка, который связывает большой и малый диаметр, а также показатель большого диаметра.
3. F=arctgf. Эта формула применяется для перевода показателя в градусы. Сегодня в большинстве случаев применяются именно градусы, так как их проще выдерживать при непосредственном проведении построений. Что касается процентов, то они зачастую указываются для возможности расчета одного из диаметров. К примеру, если соотношение составляет 20% и дан меньший диаметр, то можно быстро провести расчет большого.

Как ранее было отмечено, конусность 1:5 и другие показатели стандартизированы. Для этого применяется ГОСТ 8593-81.

На чертеже вычисления не отображаются. Как правило, для этого создается дополнительная пояснительная записка. Вычислить основные параметры довольно просто, в некоторых случаях проводится построение чертежа, после чего измеряется значение угла и другие показатели.

Уклоны и конусность — Техническое черчение

• Уклоном прямой ВС относительно прямой AB (фиг. 57, а) называется отношение:
• i=AC/AB=tga
• Конусностью называется отношение разности диаметров двух попе­речных сечений конуса к расстоянию между ними (фиг. 57,б)
• k=(D-d)/l=2tga
• Таким образом,
• k = 2i
• Уклон и конусность могут быть указаны: а) в градусах; б) дробью простой, в виде отношения двух чисел или десятичной; в) в процентах.
• Например: конусность, выраженная в градусах — 11°25’16″; отношением —  1:5; дробью —0,2; в процентах — 20%, и соответственно этому уклон в градусах — 5°42’38″; отношением — 1:10; дробью—0,1; в процентах —  10%.
• Для конусов, применяемых в машиностроении, OCT/BKC 7652 устанавливает следующий ряд нормальных конусностей — 1 :3; 1 :5; 1 :8; 1 : 10; 1 :15; 1:20; 1 :30; 1:50; 1 :100; 1:200, а также 30, 45, 60, 75, 90 и 120°.
• Допускаются в особых случаях также конусности 1:1,5; 1:7; 1:12 и 110°.

Если требуется через точку Л, лежащую на прямой AB (фиг. 57, в), провести прямую с уклоном i=l:n относительно AB, надо отложить от точки А по направлению данной прямой n произвольных единиц; в конце полученного отрезка AB восстановить перпендикуляр ЕС длиной в одну такую же единицу. Гипотенуза AС построенного прямоугольного треугольника определяет искомую прямую.

1. Для проведения прямой заданного уклона l:n через точку M, не лежащую на данной прямой AB, можно поступать двояко (фиг. 58):
2. 1)    построить в стороне прямоугольный треугольник KLN (или KLN1) с отношением катетов l:n, причём катет KL ll AB; затем через точку M провести искомую прямую MD (или MD1) параллельно гипотенузе вспомогательного треугольника KN (или LN1);

2)    опустить из точки M перпендикуляр ME на прямую AВ и при­нять его за единицу. По направлению прямой AB влево или вправо от точки E отложить n таких же отрезков; гипотенузы DM или MD1 по­строенных таким образом прямоугольных треугольников являются иско­мыми прямыми.

Построение конусности l:n относительно данной оси сводится к построению уклонов l:n/2 с каждой стороны оси.

Уклон или конусность чаще всего указывается в процентах или отношением единицы к целому числу. Рассмотрим эти способы построе­ния на примерах.

Пример 1. Требуется построить профиль сечения швеллера № 5 ОСТ 10017-39 (фиг. 59, а), если известно, что уклон его полок равен 10%

Размеры для построения берём из ОСТ 10017-39.

Проводим вертикальную прямую ek, равную h = 50 мм. Из точек e и k проводим прямые ec и kf, равные ширине полки b = 37 мм.

Ввиду того, что обе полки швеллера одинаковы, ограничимся построе­нием только одной из них. Откладываем на прямой ec от точки с отре­зок cm, равный (b-d)/2.

В точке m на перпендикуляре к прямой ec от­кладываем отрезок mn, равный t = 7 мм. Через точку n проводим прямую np параллельно ec, равную 50 мм.

• Перпендикулярно к np из точки p проводим отрезок ps, равный по длине десяти процентам отрезка np. Величина его определяется из от­ношения:
• ps/np=10/100,
• откуда
• ps=10*50/100=5 мм.

Прямая sn является искомой прямой, имеющей уклон 10% по отно­шению к ec. Дальнейшее построение профиля не представляет затруд­нений.

Отрезок np можно взять любой длины. Чем больше его величина, тем точнее будет построена прямая уклона. Однако для удобства вы­числения следует принимать отрезок np таким, чтобы длина его, выра­жаемая в миллиметрах, оканчивалась на 0 или 5.

П p и м e p 2. Построить профиль сечения двутавра № 10 ОСТ 10016-39 (фиг. 59, б), если известно, что уклон полок его равен 1:6. Размеры для построения берём из ОСТ 10016-39.

Проводим горизонтальную прямую cc, равную ширине полки b = = 68 мм. Через точку e, являющуюся серединой ширины полки, прово­дим вертикальную линию. Откладываем от точки с отрезок mс, равный

(b-d)/4. В точке m, перпендикулярно к отрезку cc, проводим прямую и

на ней откладываем отрезок mn, равный t=6,5 мм. Через точку n проводим горизонтальную прямую np, равную 30 мм, которая будет служить катетом прямоугольного треугольника. Чем длиннее катет, тем точнее будет построен уклон. Для удобства принимают длину отрезка np кратной шести, тогда второй катет будет равен целому числу. Вели­чина второго катета определяется из формулы

1. i=ps/np=1/6
2. где i — заданный уклон.
3. Подставив в формулу числовые значения, получим
4. ps=30/6=5 мм.

Откладываем в точке p под углом 90° к прямой np вычисленную длину второго катета, получим точку 5. Проводим через точки s и n прямую, которая и будет соответствовать искомой прямой, имеющей уклон 1 :6.

Построение сопряжений такое же, как и для швеллера в предыду­щем примере.