Аппликация из геометрических фигур для дошкольников, 1, 2, 3 класса (64 фото)

Аппликация из цветной бумаги по теме «Геометрические фигуры» на занятиях для детей дошкольников — младшая, средняя, старшая, подготовительная группа детского сада, 3, 4, 5, 6 лет — как сделать: инструкция

Аппликация из цветной бумаги по теме «Геометрические фигуры» на занятиях для детей дошкольников

Есть немало шаблонов для аппликаций из цветной бумаги, которые можно сделать с детьми дошкольного возраста. Такие поделки готовятся очень просто, и малышам очень интересно над ними работать. Подобное задание очень полезно в плане развития, поскольку оно знакомит ребенка с геометрическими фигурами. В детском саду, в младшей, средней, старшей, подготовительной группе детского сада, для детей 3, 4, 5, 6 лет, часто проводятся уроки по этой тематике.

Для малышей существуют специальные шаблоны, нарисованные на бумаге. Родители также сами могут создать их, изображая на листе разные фигуры и рисунки. Что нужно сделать ребенку:

• Вырезать нужное количество геометрических фигур
• Наклеить их на места, куда они подходят

Также вы можете делать аппликации по принципу, описанному ранее – выбор полностью остается за вами. Довольно интересным и простым является такой вариант поделки. Он будет иметь форму коня – очень милого и необычного. Но для начала вырежьте шаблон рисунка, по которому впоследствии ребенок будет делать аппликацию.

Аппликация из цветной бумаги по теме «Геометрические фигуры» на занятиях для детей дошкольников

Из чего делается такой конь:

1. Вырежьте 2 прямоугольника и скрепите их между собой. Они будут имитировать туловище животного.
2. Из бумажного треугольника средних размеров сделайте шею коня.
3. Для головы вам нужно вырезать круг, для мордочки – треугольник и кружочек поменьше, для глаз – совсем маленькие.
4. Ноги вырежьте в форме тонких и не очень длинных прямоугольников. Для копыт подойдут небольшие треугольники.

Хвост и гриву можно будет уже дорисовать после того, как наклеите аппликацию на основной лист бумаги. Если она вырезана из белых кусочков, то предложите ребенку раскрасить получившийся рисунок. Так процесс создания поделки будет еще более занимательным, интересным, развивающим.

Окружность

Окружность — замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра окружности), которая лежит в той же плоскости, что и кривая.

Определения:

• Радиус — отрезок, который соединяет центр окружности с любой её точкой.
• Хорда — отрезок, который соединяет какие-либо две точки окружности (AB).
• Диаметр — хорда, проходящая через центр окружности(d).  Диаметр – наибольшая хорда окружности. Наименьшей хорды окружности не существует. 
• Касательная — прямая, которая лежит в одной плоскости с окружностью и имеет с ней только одну общую точку (E)
• Секущая — прямая, которая пересекает окружность в двух различных точках.

Основные формулы:

Длина окружности: L = 2πRПлощадь круга: S = π*r2 или S = π*d2/4

где π = 3,14 (3,1415926535) – величина постоянная, где r-радиус, d –диаметр, L – длина окружности, S-площадь.

С какого возраста можно начинать учить с ребенком геометрические фигуры

По мнению ученых, обучать малыша следует с самого рождения, при этом его проводят в несколько этапов:

После рождения малыш почти ничего не запоминает, однако приучается смотреть на мир во всех его аспектах. В это время рекомендуется разговаривать с младенцем, проговаривая каждую фигуру, читать небольшие детские стихи, петь песни.
Когда ребенку исполнится 6 месяцев, он постарается узнать о мире побольше. Для этого он будет трогать и покусывать предметы

Важно подобрать правильные игрушки. Подойдет набор мягких квадратов, на которых нарисованы цветы, бабочки, птички.
Следующий этап начинается тогда, когда малыш учится говорить

Необходимо проговаривать все названия фигур, начиная с самых простых (круг, треугольник, квадрат). Затем придет черед трапеции, прямоугольника и других. На этом этапе поможет игрушечная пирамидка, пластмассовые кубики, из которых строят башню, и рисование.

Изучение геометрических фигур с ребенком можно начинать с самого раннего возраста, можно с рождения ребенка, используя разные методики.

Изучение геометрических фигур: названия, форма, цвет, размер

С возрастом ребенок должен узнавать все больше фигур и цветов.

К 2 годам необходимо знать:

• треугольник;
• квадрат;
• круг.

В этом же возрасте нужно знать основные цвета:

• синий;
• красный;
• желтый;
• зеленый;
• белый.

К 2 годам ребенок должен знать основные геометрические фигуры и цвета

Некоторые дети в 2 года знают несколько больше цветов:

• оранжевый;
• фиолетовый;
• черный;
• розовый.

К 6 годам ребенок узнает о более сложных, комбинированных цветах и оттенках, знакомится с составными (состоящими из основных) фигурами.

Дети обучаются через игры, они бывают разной сложности, поэтому давать их ребенку рекомендуется в следующей последовательности:

• Нарисованные на картоне круги, треугольники, квадраты разных размеров и цветов. Называйте изображения своими именами, проговаривая их вслух.
• Нарисовать на картоне только контуры фигур, причем все контуры должны быть разных цветов, чтобы малыш обводил их соответствующими цветами, раскрашивал и проговаривал названия вслух. В возрасте от 2 лет следует начинать сравнивать размеры.

Сортер с геометрическими фигурами помогает детям в их изучении

Вырезать фигуры и разложить на видных местах в доме, чтобы малыш искал рисунки. Каждый раз, когда ребенок находит изображение, он должен назвать следующие характеристики: фигуру, цвет и размер.
Игровые наборы, предназначенные для изучения выше перечисленного. Например, пирамидка, грибы разных цветов и размеров на подставке, мозаика и другие

Такие игры развлекут ребенка, привлечет его внимание.
Поиск геометрических фигур в окружающем мире. Например, стол – это прямоугольник, шкатулка – квадрат, а мячик – круг

Рекомендуется рассматривать и более сложные формы: стакан – цилиндр, а праздничный колпак – пирамида.

Разработано множество методик, предназначенных для изучения фигур и цветов. Они рассчитаны для детей разного возраста, а также учитывают их любимые занятия.

Рисование геометрических фигур | Artstudi.ru Художественная студия

С данного урока начинается наша программа обучения рисунку. В этом задании рассматривается тема рисования простых геометрических фигур.

Рисование геометрических фигур можно сравнить с изучением алфавита для того, кто осваивает иностранный язык. Геометрические формы – первая стадия построения объекта любой сложности. Это хорошо видно в компьютерном моделировании, где построение трехмерного космического корабля начинается с простого кубика. В рисунке все изображаемые предметы всегда состоят или делятся на простые геометрические формы. Для обучения рисунку это значит ровно одно: научившись правильно изображать геометрические фигуры, научитесь рисовать все остальное.

Построение геометрических фигур.

Начинать построение нужно с анализа модели, образно говоря, проникнуть вглубь конструкции на уровень вершин и линий. Это значит, представить геометрическую фигуру в виде каркаса, состоящего только из линий и вершин (место пересечения линий), путем воображаемого удаления плоскостей. Важным методологическим приемом является изображение невидимых, но существующих линий. Закрепление такого подхода с первых уроков станет полезным приемом для рисования более сложных моделей.

Далее, под руководством педагога наметить на листе расположение линий и вершин, легкими, скользящими движениями, без нажима на карандаш.Положению рисунка на листе стоит уделить отдельное внимание по нескольким причинам:

• Нахождение центральной оси листа поможет при дальнейшем построении как отправная точка для вертикальных линий конструкции.
• Определение линии горизонта, для правильного изображения перспективы.
• Учет светотеневой моделировки, собственные и падающие тени, чтобы они поместились в пространстве листа и уравновешивали друг друга.

После нанесения основных конструктивных линий следует детальная прорисовка видимых ребер предмета, в случае с объектами вращения (шар, конус) это внешние края формы.

За конструктивной частью следует штриховая моделировка. На уроках рисунка мы подробно разбираем правила и технику нанесения штрихов на геометрические предметы.

Профессиональное обучение рисунку легко сравнить с уроками музыки, где сухие правила и точные схемы в конечном итоге приводят будущего композитора к творческим произведениям. Так и в рисунке законы построения форм, правила перспективы, схемы расположения теней помогают художнику создавать уникальные шедевры.

Отчего опытные художники могут быстро наносить сложные рисунки, не тратя много времени на разметку, построение? Потому что вначале крепко заучили правила и каноны, и теперь достаточно ясно представляют строение любой формы

Схематичный рисунок освобождает внимание автора от конструкции и сосредотачивает фокус на композиции, идее, образе своего творения. Существует мнение, что заученные схемы не дадут художнику полностью раскрыться.Стоит посмотреть, с чего начинали такие креативные мастера как Пикассо и Дали, чтобы понять ошибочность данного суждения

Но лучшей проверкой станет обучение в нашей студии, где вы на практике убедитесь в плюсах академического подхода.

Ждем Вас в нашей художественной студии!

Четырёхугольник

Четырёхугольник — это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин) и четырёх отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три точки не лежат на одной прямой.

Основные свойства:

• Сумма углов четырёхугольника равна 360°
• Не существует четырёхугольников, у которых все углы острые или все углы тупые.
• Каждый угол четырёхугольника всегда меньше суммы трёх остальных углов.
• Каждая сторона четырёхугольника всегда меньше суммы трёх остальных сторон.

В четырёхугольник можно вписать окружность, если суммы его противолежащих сторон равны. Центр вписанной в четырёхугольник окружности является точкой пересечения биссектрис всех четырёх углов этого четырёхугольника.

Четырёхугольник можно описать окружностью, если сумма его противолежащих углов равна 180°.Центр описанной около четырёхугольника окружности является точкой пересечения всех четырёх серединных перпендикуляров сторон этого четырёхугольника.

Виды аппликации

Аппликация бывает простая, сложная, комбинированная. Можно начать с самых простых предметов и развивать навык до сложных композиций, составленных из разных материалов.

Рассмотрим несколько видов геометрической аппликации:

• нарисовать рисунок – заготовку, разрезать его на несколько геометрических фигур, сложить детали в коробку и вместе с ребенком склеить рисунок обратно. Для облегчения задачи, оставить контур рисунка, карандашом пометить расположение деталей;
• нарисовать рисунок, без прорисовки деталей. Линиями обозначить цветовые контуры внутри картинки. Вырезать необходимое количество штук мелких геометрических фигур (разноцветные треугольники, квадраты и т.д.), закрыть фигурой нужного цвета, соответствующий сектор на шаблоне;
• нарисовать и вырезать несколько геометрических фигур разной формы и цвета. Из них собрать разные фигурки и приклеить на лист основу.

С ребенком постарше можно создать объемные фигуры аппликацию. Эффект объема получается за счет того, что некоторые детали композиции не проклеиваются, а загибаются определенным образом.

Организация процесса

Геометрическая аппликация не требует от взрослых серьезных художественных навыков для организации процесса детского творчества. Главное — обеспечить малышей всеми необходимыми материалами и инструментами, организовать безопасное и удобное для работы пространство.

Для самых маленьких.

Чтобы детки 2–4 лет успешно сделали аппликацию, для них нужно подготовить рисунок с четкими контурами и вырезать соответствующее количество деталей. При этом им может потребоваться личный пример старшего, показывающего на такой же заготовке, что, куда и как наклеивать.

Для детей 4–5 лет.

В этом возрасте ребята уже могут без готовых контуров расположить геометрические фигуры на листе, глядя на образец. Детали с прямыми линиями, например треугольники, им можно поручить вырезать самостоятельно из расчерченных листов цветной бумаги. При этом следует позаботиться о том, чтобы ножницы были безопасными — с закругленными концами.

Для старших дошкольников.

В 6–7 лет дети способны сами обводить несложные шаблоны и вырезать детали аппликации. В этом возрасте полезно предоставлять им самостоятельный выбор цветовой гаммы поделки: например, при изображении цветов, геометрических узоров, бабочек. Это помогает им научиться сочетать цвета и развивает творческие способности.

Бумага

Основной материал для создания плоских поделок — бумага. Она используется для фона и для вырезания геометрических элементов. Для основы можно выбрать цветной картон или плотную бумагу. Мелкие детали вырезаются из двусторонней бумаги средней плотности. Яркие аппликации получаются из цветных листов для офиса.

Клей

Клеящий состав подбирается в соответствии с возрастом ребёнка. Малышам 2 лет для работы подходит клейстер из картофельного крахмала или пшеничной муки. Такой клей не вызывает аллергии и не причинит вреда в случае проглатывания, поэтому его можно намазывать на маленькие детали пальцами.

Для изготовления 1 литра клейстера 5 столовых ложек сухого вещества разводят небольшим количеством воды до образования однородной пасты. Затем её разводят оставшейся жидкостью. Раствор кипятят на медленном огне до уплотнения массы и процеживают через сито.

Детям 3-4 лет удобно работать с канцелярским клеем в виде карандаша

При его выборе следует особое внимание уделить качеству продукта. Он должен наноситься ровным слоем, не оставлять комков на бумаге и не иметь резкого запаха

ПВА и кисти для его нанесения используются ребятами со старшей группы детского сада. Работа с жидким клеем требует достаточного развития мелкой моторики, внимания и аккуратности. Кисти для нанесения клеящего вещества на бумагу выбираются средней жёсткости. Их величина зависит размера рабочей детали.

Ножницы

Главное требование к ножницам, которыми пользуются дети — безопасность. Для ребёнка покупают ножницы с круглыми концами. Перед началом детского творчества взрослый человек должен проверить качество функционирования механизма, так как ножницы с неразработанными рычагами могут быть опасны для ребёнка.

Длина лезвия детских ножниц составляет примерно 10-12 см. При вырезании больших деталей можно использовать более длинные модели.

Важно! Прежде чем учить детей работать ножницами, необходимо познакомить их с техникой безопасности, состоящей в следующем:

1. Во время работы нельзя ими размахивать и играть.
2. Передавать их следует кольцами вперёд, взяв за сложенные лезвия.
3. После использования инструменты убираются на место.
4. Хранят ножницы в коробках или высоких подставках кольцами вверх.

Аппликации в виде насекомых

Аппликации в виде насекомых выполнять немного сложнее. Здесь больше мелких деталей, что потребует проявления усидчивости, чтобы довести работу до конца.

Модель 1 «Божья коровка»

Аппликацию в виде божьей коровки могут сделать детки старшего дошкольного возраста. Она направлена на развитие фантазии и художественного вкуса, кроме того, работа с небольшими элементами полезна для мелкой моторики рук.

Для аппликации нам понадобятся:

• картон зелёного цвета;
• цветная двусторонняя бумага красного, чёрного и белого тона;
• ножницы, клей и фломастер чёрного цвета;
• простой карандаш;
• эскиз.

Порядок работы:

Сначала, при помощи шаблона нарисовать и вырезать на листе чёрной бумаги круги.

Из чёрных кругов делаем туловище божьей коровки и её голову

Затем, из бумаги красного цвета по шаблону вырезать 2 круга.

Сложить красные круги пополам – у нас получатся крылья

На картоне зелёного цвета нарисовать листочек и вырезать его ножницами.

Листочек необходимо сделать с неровными краями

После этого, на листочек приклеить туловище божьей коровки и её голову.

Туловище должно заходить на голову внахлёст

Далее, приклеить к заготовке крылья, после чего, закрепить на них клеем 6 кружков, предварительно вырезанных из бумаги чёрного цвета.

Вырезать глазки из белой бумаги и приклеить их, дорисовать зрачки, усики и лапки фломастером чёрного цвета.

Вот такая объёмная божья коровка должна получиться

Модель 2 «Добродушная пчёлка»

Аппликация «Пчёлка» потребует максимальной концентрации внимания. Ребятам предстоит не только аккуратно вырезать детали, но и правильно их сопоставить и наклеить.

Ребёнку будет интересно подбирать фигурки по цвету и комбинировать их

Предлагаем сделать вместе с детьми ещё несколько аппликаций в виде насекомых.

Ромб

Ромб — это параллелограмм, у которого все стороны равны.

Основные формулы:

Периметр: P=4*aПлощадь по стороне и высоте: S=a*hПлощадь по диагоналям: S = (d₁*d₂)/2Радиус окружности, вписанной в ромб: r=h/2 или  r =(d₁*d₂)/4aПлощадь по стороне и радиусу вписанной окружности: S=2*a*rПлощадь по стороне и углу: S = a2 · sin α

где a — длина стороны, d₁, d₂ –диагонали, P-периметр, S-площадь, h -высота, проведенная к противоположной сторонеα — угол между сторонами ромба

Свойства:

• Диагонали ромба пересекаются под прямым углом и являются биссектрисами его углов.
• В любой ромб можно вписать окружность с центром в точке пересечения его диагоналей. Радиус окружности: r=h/2 или r = d₁*d₂/4a.

Как сделать аппликацию из треугольников

Материалы для выполнения аппликации:

• листы цветной бумаги (двух цветов, например – красный и желтый),
• плотные листы белой бумаги,
• клей (клеящий карандаш для малышей),
• кисточки,
• ножницы (для взрослого).

Аппликация из треугольников “Рыбка”

Для детей, которые не могут самостоятельно вырезать, родитель (воспитатель) вырезает по шаблону из цветной бумаги геометрические фигуры – треугольники. Треугольники будут разного размера.
Каждому ребенку (в саду) раздают коробочки с вырезанными цветными деталями, лист белой плотной бумаги, клей.
Детям следует показать образец, чтобы они знали какую аппликацию они будут выполнять на занятии

Нужно обратить внимание на фигуру (сказать, что это треугольники), размер деталей (попросить найти маленькие и большие), спросить какого цвета детали у них в коробочках.
После этого нужно рассказать что аппликация эта непростая. Чтобы она получилась нужно правильно разложить треугольнички на своем листе бумаги

Чтобы дети подумали можно дать им нерасчерченные шаблоны. Если времени на это задание нет, то нужно показать шаблоны по которым дети соберут фигурку.
Пусть ребенок сам выберет шаблон. Можно даже предложить детям собрать по очереди все шаблоны (без клея, просто размещая треугольники на бумаге). Это один из уроков на логику.
После того как шаблон рыбки выбран, воспитатель показывает как намазывать клеем треугольники цветной бумаги и как правильно прилеплять их к листу белой бумаги (строго по центру чтобы было красиво). Часто дети начинают приклеивать треугольники, не разложив сначала всю фигуру – в итоге хвост или плавнички рыбки вылезают за края листа.

7. Родитель (воспитатель) обязательно должен не только похвалить ребенка за выполненную работу, но и указать на ошибки (если таковые имеются). 8. После просушки работу можно поставить на выставку или на полочку в комнате ребенка.

Аппликация из треугольников “Елочка”

Эта аппликация похожа на вышеописанную, но несколько сложнее. Детали приклеиваются в определенной последовательности и с перекрытием.

Материалы для выполнения аппликации:

• листы цветной бумаги (двух цветов – зеленый и коричневый),
• плотные листы белой бумаги,
• клей (клеящий карандаш для малышей),
• кисточки,
• ножницы (для взрослого).

Родитель (воспитатель) как и в аппликации “Рыбка” вырезает треугольники из цветной бумаги и раздает их ребятам.
Перед занятием детям следует показать готовую работу, сказать какая она красивая и интересная

Далее нужно обратить внимание детей, на то, что эта аппликация с хитростью. Чтобы получилось красиво, нужно приклеить треугольники с перекрытием.
Дети раскладывают треугольники на листе самостоятельно

Взрослый объясняет в каком порядке следует наклеивать фигурки, чтобы получилась красивая елочка.
Дети по шаблону наклеивают треугольники на белый лист бумаги (взрослый корректирует работу, помогает исправить ошибки). Обязательно в конце занятия нужно похвалить ребенка.
Готовые работы высушиваются под прессом, а потом выставляются на выставке.

Аппликации из геометрических фигур

А вообще аппликации можно делать из любых геометрических фигур. Треугольники мы уже разобрали, но есть много и других фигур: круги, квадраты, прямоугольники, ромбы. Давайте вместе с детьми попробуем собрать веселые аппликации по готовой схеме.

Вот мальчишкам больше нравятся поделки с самой разной техникой и машинками. Попробуйте предложить малышам – мальчикам аппликации с подъемным краном, машинкой, паровозом, корабликом или ракетой.

Все, что требуется от родителя – это распечатать на листочке бумаги шаблон. Малыш по образцу вырезает детали и наклеивает их на основу. Картинку можно дополнить надписью или раскрасить фон цветными карандашами или фломастерами.

Я знаю детей, и сразу вас предупрежу – если такие развивающие занятия понравились ребенку, то одним шаблоном вы не отделаетесь. Лучше сразу распечатать несколько.

Девочки тоже не останутся без аппликаций. Им можно предложить шаблоны для аппликации с животными. Технология выполнения таких аппликаций не отличается от вышеописанного варианта для машин. Распечатываете шаблон, ребенок вырезает из бумаги геометрические фигуры и наклеивает их на контур. В итоге красивая и занимательная аппликация с мышкой, лисой, белочкой, лошадкой и другими зверями.

Не забывайте, нужно не просто вручить ребенку картинку и н6ожницы с клеем. Обязательно повторите названия геометрических фигур, а заодно и цветов. Помогите и подскажите малышу, если он забыл как называется фигура. Вот тогда ваши занятия будут настоящим развивающим творчеством.

Занятия геометрической аппликацией из простых фигур (треугольников) доступны и просты. Поверьте, эти занятия придутся по душе ребятам.

Вдохновляющие примеры геометрических иллюстраций

Как бы вы в школе не относились к геометрии, нельзя отрицать, что геометрия и искусство связаны друг с другом. Не зная геометрии человек бы не смог бы создать известных во всём мире египетских пирамид, Малевич не нарисовал бы свой «Чёрный квадрат». Геометрия несет в мир человека много прекрасного и интересного. Геометрические иллюстрации являются популярной тенденцией дизайна. Давайте посмотрим, как с помощью геометрических форм иллюстраторы создают удивительные абстракции, иллюстрации животных и портреты людей.  

Nacho Gil 

The Animals

Hip Hop

MARTA CERDÀ ALIMBAU 

Maria Grønlund 

Cat Lines

MARTA CERDÀ ALIMBAU 

Thomas Wilder 

tadaomi shibuya 

Marinos 

  \

James White

Kevin Harald Campean 

Paula Rusu 

mat gigliotti

Marcelo Schultz 

Cesar Gomez

Érico Santana 

Jose Ortiz 

Были использованы материалы: creativenerds.co.uk

Смотрите также:

Идеи поделок для самых маленьких детей

Расширить детский кругозор, развить творчество и фантазию, закрепить знание форм и размеров помогут простые и легкие аппликации из кругов. Используя простые геометрические формы круга и полукруга легко создать красивые поделки, которые используются для украшения детской или передаются для участия в выставках в садике:

• божья коровка. Аппликация может быть плоской и объемной, такая идея поможет ребенку освоить композицию и контрастные цвета;
• веселая гусеница. Разноцветная гусеница может быть любой длины и благодаря такой поделке ребенок сможет закрепить знание цветов;
• цветок на пригорке. Цветок из кругов и листочек из полукругов, высаженные на полукруге пригорке используются для изучения масштаба.

Если малышу трудно самостоятельно пройти все этапы изготовления поделки родители могут сделать для него заготовки кружки. Такой вид творчества как аппликация из кругов интересна для детей дошкольного возраста и школьников младших классов, помогает развивать фантазию и закреплять усвоенный в учебном процессе материал.

Аппликации в виде птичек и зверушек

Аппликации птичек и зверушек делать не менее увлекательно, чем домик и транспорт. Здесь уже большее количество мелких элементов, поэтому понадобится помощь старших. Техника предназначена для деток в возрасте 5-6 лет, принцип работы аналогичен предыдущим мастер-классам.

Модель 1 «Курочка с цыплёнком»

Можно не просто сделать аппликацию вместе с ребёнком, но и провести весь процесс в игровой форме. В качестве примера рассмотрим поделку цыплёнка.

Нам понадобятся:

• белый и цветной картон;
• ножницы и клей;
• фломастеры, можно взять и краски.

Приступаем к работе.

1. На белом картоне нарисовать солнце, курочку, цыплят. Можно добавить травку и облака.
2. Из цветного картона вырезать курочку, солнышко и 4 жёлтых кружочка. Они потом станут цыплятами и солнцем.
3. На стол положить эскиз из белого картона. Предложить ребёнку рассказать о том, кого не хватает на картинке. Детки в этом возрасте должны догадаться, что один кружок – это солнышко, а остальные – цыплята. Далее следует промазать клеем каждый элемент и приклеить его на своё место.

Предлагаем сделать с детками ещё несколько интересных и несложных поделок птичек.

Модель 2 – поиграем в угадайку – аппликация «Кошка с котёнком»

Можно с ребёнком поиграть в угадайку, для неё потребуется заранее подготовить геометрические фигурки. Ребёнок должен самостоятельно их вырезать, определить, какое это животное, и правильно приклеить элементы на основу:

• треугольники – это ушки:
• овалы – это хвостик и туловище;
• кружочки – голова, можно нарисовать или наклеить глазки;
• прямоугольники – лапки.

Результатом работы станет итоговая картинка, в которой можно будет узнать кошку с котёнком.

Не стоит останавливаться на достигнутом, необходимо поручить ребёнку изготовить более сложные поделки.

Простейшие картинки

Детки 1-2 годиков только знакомятся с окружающим миром

Их важно обучить наклеиванию, исключая чёткую композицию. Занятие проводится в виде игры

Мишка-жонглёр

Следует придумать историю, как медведь потерял мячики для жонглирования. Целью выступает знакомство малышей с кругом, закрепление знаний об оттенках, формирование навыков обращения с клеящим веществом. Потребуется:

• кружки разного размера и цветные листы;
• медвежий образ, как яркая наклейка;
• картон;
• клей, в составе которого крахмал или мука;
• сухая и влажная салфетка.

Рассказывая случай, как весёлый медвежонок растерял мячики, наклейте персонаж. Помогите ребёнку отыскать эти шары, отличающиеся объёмом и тоном. Теперь маленькому мастеру предстоит самому, смазывая детали от центральной части к краю, расположить их вокруг Топтыгина и, используя сухую тряпочку, прижать к основанию.

Блюдо с фруктами

Это более сложная поделка, закрепляющая полученные знания. Рисуется и вырезается тарелка или корзинка. В неё детки осуществляют доставку изображений яблок, груш, винограда, сопоставляя их по геометрическим конфигурациям. После этого повторяются названия вкусных предметов и цветовая гамма. Тут же можно попробовать сделать гусеницу, которая не против того, чтобы полакомиться ими.

Создание аппликаций из геометрических фигурок

Для начала ребёнка надо познакомить с геометрией, показав и объяснив различие предметов по форме, чтобы, работая, он самостоятельно подбирал детали. Перед началом процесса, подготовьте рабочую область:

1. Освободите стол, покрыв его защитной плёнкой.
2. Предварительно заготовьте нужные элементы.
3. Пользуйтесь безопасными ножницами, имеющими тупые концы.
4. Приготовьте картонку или иную плотную основу.
5. Обзаведитесь клеем, цветной бумагой насыщенных тонов.

Малыша надо ознакомить с последовательностью действий и техникой приклеивания заготовок. Проводить работу желательно совместно.

Прямоугольник

Прямоугольник — четырехугольник, у которого все углы прямые.

Основные формулы:

Периметр: P=(a+b)*2Площадь по сторонам: S = a*bПлощадь по диагонали и углу между ними: S =  d²* sin γ. / 2Стороны и диагональ связаны соотношением: d=√(a2+b2)/2 (теорема Пифагора)Радиус описанной окружности: R= √(a2+b2)/2 (теорема Пифагора)

где a, b — длины сторон прямоугольника, d-диагональ, P-периметр, S-площадьγ – угол между диагоналями*Корень квадратный вычисляется из всего, что стоит в скобках после знака √, например, √(a2+b2) – корень квадратный из (a2+b2).

Свойства:

• Диагонали прямоугольника равны и делятся точкой пересечения пополам.
• Около любого прямоугольника можно описать окружность с центром в точке пересечения его диагоналей и радиусом, который равен половине диагонали.

Упражнения по геометрии для детей старшей группы

Предлагаем вашему вниманию развивающее упражнения для детей 5 — 6 лет, которое в доступной и занимательной форме поможет ребенку освоить основы геометрии, а также развить зрительное и слуховое восприятие, произвольное внимание, память, логическое и пространственное мышление. Занятие с ребенком этого возраста должно длиться не более 25 — 30 минут

Объясните малышу задание, при необходимости помогите в его выполнении. Убедитесь, что задание выполнено верно

Занятие с ребенком этого возраста должно длиться не более 25 — 30 минут. Объясните малышу задание, при необходимости помогите в его выполнении. Убедитесь, что задание выполнено верно.

Для работы малышу потребуются цветные карандаши или фломастеры.

Не забудьте проследить за правильной осанкой малыша, а также похвалить его за старание.

Успехов вам и вашим детям!

Задание №1

Раскрась фигуры так, чтобы круг лежал на квадрате.

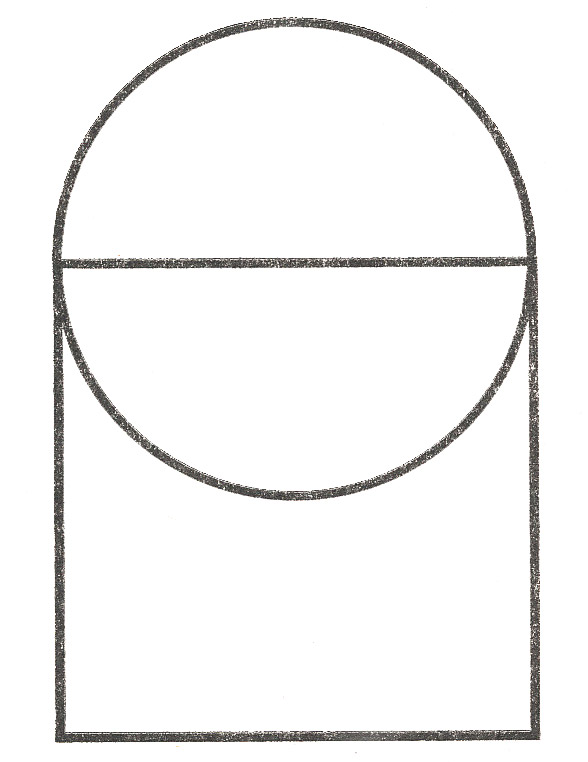
Задание №2

Раскрась фигуры так, чтобы треугольник лежал на трапеции.

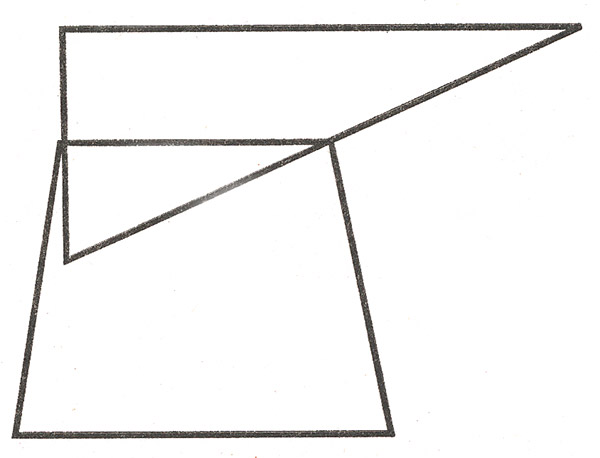
Задание №3

Раскрась фигуры так, чтобы овал лежал на ромбе.

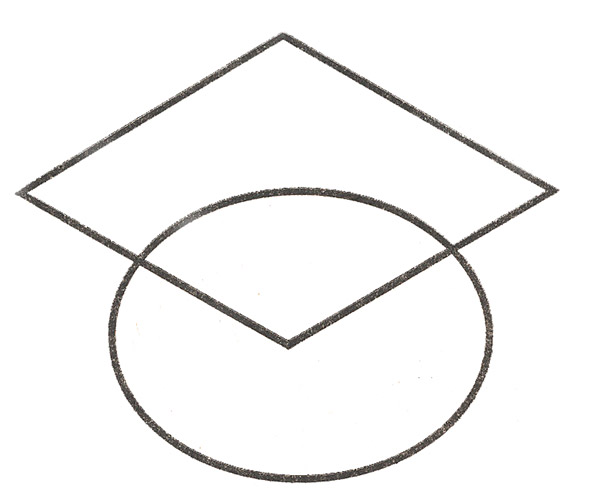
Задание №4

Раскрась фигуры так, чтобы пятиугольник лежал на прямоугольнике.

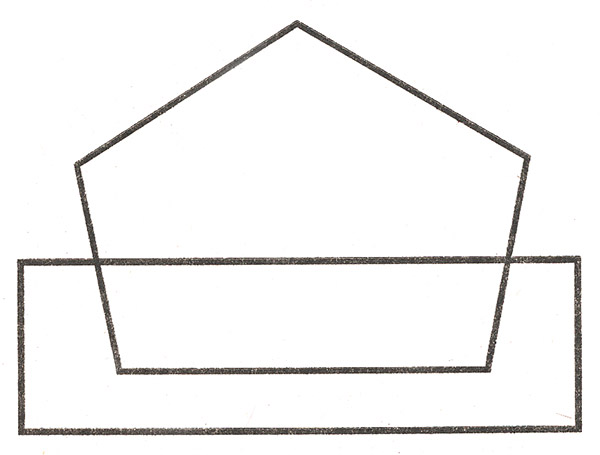
Задание №5

Найди продолжение каждой цепочки. Соедини начало и конец цепочки. Раскрась их. Из каких фигур они состоят?

Задание №6

Нарисуй в пустых клетках фигуры, на которые похожи эти предметы. Назови фигуры.

Задание №7

Соедини предметы линиями с похожими на них геометрическими телами.

Задание №8

Обведи прямые линии красным цветом, кривые – синим, ломаные – зелёным.

Задание №9

Выполни штриховку круга вертикальными линиями, квадрата – горизонтальными, треугольника – наклонными.

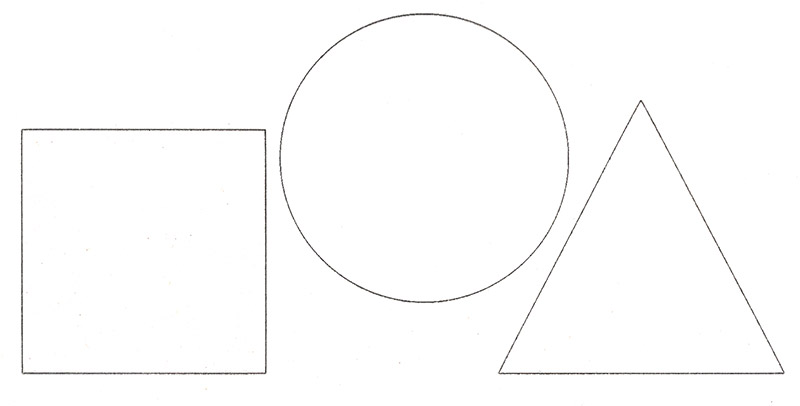
Задание №10

Здесь нарисованы разные линии, и среди них — ломаные. Найди и сосчитай ломаные линии. Сосчитай их звенья. Посмотри, что нарисовал художник на концах ломаных линий. Нарисуй на противоположных их концах такие же предметы.

Задание №11

Продолжи ломаные линии так, чтобы получились различные предметы. Назови, что у тебя получилось.

Задание №12

При помощи линейки соедини точки так, чтобы получились многоугольники. Многоугольник, у которого все углы прямые, раскрась красным цветом. Многоугольник, у которого все углы тупые, раскрась синим цветом. Объясни, почему одна фигура осталась нераскрашенной.

Задание №13

Поставь цветными карандашами точки в местах пересечения линий.

Задание №14

Обведи в каждом ряду лишнюю линию. Объясни, чем она отличается от других.

Задание №15

Обведи прямые углы красным карандашом, острые зеленым, а тупые — синим.

Задание №16

Красным карандашом обозначь вершины многоугольников, а синим — стороны многоугольников.

Задание №17

Раскрась фигуры, используя обозначения.

Задание №18

Раскрась фигуры разными цветами, используя обозначения.

Кот из ватных дисков

Приготовить плотный бумажный лист. На нем простым карандашом нарисовать рисунок из геометрических фигур. В данном случае – стилизованного кота из кругов и полукругов, равных диаметру ватного диска. Рисунок прорисовывать не нужно, достаточно наметить легкий контур.

Смазать ватный диск с одной стороны клеем и поместить в нужное место на бумаге с рисунком – шаблоном.

Туловище и голова – 2 диска, лапы – разрезанный пополам диск, уши – маленькие треугольники, хвост – вырезанный по спирали кусочек диска.

Из черной бумаги вырезать кружок – нос, нарисовать маркером глаза. Первая аппликация готова!

Треугольник

Треугольник – это геометрическая фигура, которая состоит из трёх точек, не лежащих на одной прямой (вершин треугольника) и трёх отрезков с концами в этих точках (сторон треугольника).

Определения:

• Углами (внутренними углами) треугольника называются три угла, каждый из которых образован лучами, выходящими из вершин треугольника и проходящими через две другие вершины.
• Высота треугольника — перпендикуляр, опущенный из любой вершины треугольника на противолежащую сторону или на продолжение стороны
• Медиана треугольника — отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.
• Биссектрисой треугольника, проведённой из данной вершины, называется отрезок биссектрисы угла треугольника, соединяющий эту вершину с точкой на противолежащей стороне
• Равные треугольники – треугольники, у которых соответствующие стороны равны и соответствующие углы равны
• Равнобедренный треугольник— треугольник, у которого две стороны равны. Равные стороны называют боковыми сторонами, а третью – основанием равнобедренного треугольника.
• Равносторонний или правильный треугольник – треугольник, у которого все стороны равны.
• Прямоугольный треугольник — треугольник, у которого есть прямой угол. Стороны, прилежащие к прямому углу, называются катетами, противолежащая прямому углу – гипотенузой.

Основные формулы:

Периметр: P=a+b+cПлощадь по стороне и высоте: S=(a*h)/2Площадь: по сторонам и углу между ними:  S=(a*b)/2* sin γ                        по трем сторонам и радиусу описанной окружности: S=(a*b*c)/4R                        по трем сторонам и радиусу вписанной окружности: S=(a+b+c)/2*rПлощадь прямоугольного треугольника: S=(a*b)/2Стороны прямоугольного треугольника: c2=a2+b2 (Теорема Пифагора)

где a,b, c — стороны (a,b –катеты , с – гипотенуза в случае прямоугольного треугольника)d₁, d₂ –диагонали, h -высота, проведенная к противоположной стороне, P-периметр, S-площадь, γ  — угол между сторонами a и br — радиус вписанной окружности, R — радиус описанной окружности

Свойства:

• В треугольнике против большего угла лежит большая сторона, против большей стороны лежит больший угол.
• Сумма углов треугольника равна 180°:
• Длина каждой стороны треугольника больше разности и меньше суммы длин двух других сторон: |a-b| <c<a+b
• Высоты треугольника пересекаются в одной точке, которая называется ортоцентром треугольника.
• Медиана делит треугольник на два равновеликих (с равными площадями) треугольника. Три медианы треугольника делят его на шесть равновеликих треугольников
• Биссектрисы внутренних углов треугольника пересекаются в одной точке, находящейся внутри треугольника, равноудалённой от трёх его сторон, которая является центром окружности, вписанной в данный треугольник
• В равнобедренном треугольнике углы при основании равны. В равнобедренном треугольнике медиана, проведённая к основанию, является и биссектрисой и высотой.
• Все углы равностороннего треугольника равны 60°. Каждая медиана равностороннего треугольника совпадает с биссектрисой и высотой.
• В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов: c2=a2+b2 (Теорема Пифагора).В прямоугольном треугольнике гипотенуза всегда больше любого из катетов.