Золотое сечение в строительстве

Золотое сечение в дизайне интерьера

При планировании пространства рисуется планировка, которую разбивают на части по принципу золотой спирали. Зонирование пространства, производится в точном соответствии с точками пересечения основных линий – в этих точках будет находится мебель, ширмы, экраны и т. д.

Когда проектирует дом, то тоже придерживаются необходимых правил. Так, отношение самой большой комнаты к площади квартиры равняется как 0,62 к 1, меньшая с таким же соотношением к площади большой, кухня — к меньшей комнате, прихожая к кухне, санузел к прихожей, балкон – к санузлу.

Использование золотых пропорций в интерьере вашего дома, квартиры

Смотря на картинку ниже, сразу же бросается в глаза едва уловимая асимметрия, и легкий беспорядок. Золотое сечение помогает оформить интерьер, который будет давать чувство спокойствия и уюта. 

Красиво обустроенный домашний интерьерИсточник 1zoom.me

Следует запомнить, что идеальным по форме помещением является, такое у которого соотношение ширины к длине равно 5 к 8, или 1 к 1,62.

При проектировании первых многоквартирных домов, в начале прошлого века, использовалась система антропометрических пропорций, придуманная архитектором Ле Корбюзье.

Модулор Ле Корбюзье Источник /www.metalocus.es

Так называемый «модулор» представлял собой фигурку человека с поднятой рукой, рост и все пропорции которого, равнялись усредненным, реальным параметрам человеческого тела.

 Это еще раз доказывает, что наиболее удобным для человека жильем является дом, спроектированный в соответствии с законами божественной пропорции, которые проявляется в природе и в частности в человеческом теле.

Расстановка мебели по законам золотого сечения

Самое главное, что вам нужно запомнить это соотношение 2:3.

Для начала, необходимо визуально разделить пространство на две части: большая, которая составит две трети от общей площади, будет содержать мебель и станет основной зоной, и меньшая, предназначенная для вторичных функций, как отдельный уголок, или место для хранения.

Видео описание

В этом видео представлен пример применения принципа золотого сечения в обстановке дома:

Выбор цвета по правилам золотого сечения

Обычно при выборе цветовой гаммы пользуются соотношением 10-30-60, которое основывается на золотом сечении.

Таким образом, пространство должно состоять из трёх цветов: первый – доминирующий, который будет охватывать 60% комнаты, этот цвет припадает на стены и пол.

За ним следует второй, который составляет 30% — это мебель. И третий, составляющий 10%, используется для небольших предметов, тот же декор.

Правильное соотношение занимаемой мебелью площади Источник salexplorer.com

Подвесной декор

Разделите свободную площадь стены на три равные части по горизонтали и вертикали, прямоугольник, который окажется внутри и будет привлекать основное внимание гостей. 

Демонстрация гармоничного подвесного декораИсточник yandex.net

Золотое сечение в мебели

Необходимое число и нужные размеры мебели определяют, отталкиваясь от габаритов самых крупных ее представителей – шкафов, диванов, столов, и т. д. Например, если шкаф-стенка занимает две трети от всей площади комнаты, тогда диван-кровать должен быть в пределах 2/3 от величины шкафа. По тому же принципу строится соотношение размеров стола к дивану, кресел к столу, стульев к креслам и т.д. 

Гармоничная расстановка мебелиИсточник decoratw.com

То же самое и с декором, большие предметы комбинируются с более мелкими, с сохранением соотношения золотой пропорции.

Есть фирмы, которые выпускают целые наборы мебели, спроектированные, с уже правильным соотношением размеров отдельных элементов набора.

Уютный интерьер комнаты Источник yandex.net

Видео описание

Смотрите в видео примеры применения правила золотого сечения в интерьере:

Заключение

Золотое сечение — это соотношение одной величины к другой на 1,618. Применяется в искусстве, дизайне логотипов и других областях жизни людей. Но первоначально этот принцип был выведен из природы: строения ракушки, уха человека, вселенной, ДНК.

У людей, которые знают правило золотого сечения, как правило, не возникает трудностей с правильной и гармоничной расстановкой мебели в комнате, и различных элементов декора. Также эта информация помогает и в ландшафтном дизайне, более эстетично и правильно благоустроить сад и огород, детскую площадку.

Золотое сечение в строении микромиров

Геометрические фигуры не ограничиваются только лишь треугольником, квадратом, пяти- или шестиугольником. Если соединить эти фигуры различным образом между собой, то мы получим новые трехмерные геометрические фигуры. Примерами этому служат такие фигуры как куб или пирамида. Однако кроме них существуют также другие трехмерные фигуры, с которыми нам не приходилось встречаться в повседневной жизни, и названия которых мы слышим, возможно, впервые. Среди таких трехмерных фигур можно назвать тетраэдр (правильная четырехсторонняя фигура), октаэдр, додекаэдр, икосаэдр и т.п. Додекаэдр состоит из 13-ти пятиугольников, икосаэдр из 20-и треугольников. Математики отмечают, что эти фигуры математически очень легко трансформируются, и трансформация их происходит в соответствии с формулой логарифмической спирали золотого сечения.

В микромире трехмерные логарифмические формы, построенные по золотым пропорциям, распространены повсеместно. К примеру, многие вирусы имеют трехмерную геометрическую форму икосаэдра. Пожалуй, самый известный из таких вирусов — вирус Adeno. Белковая оболочка вируса Адено формируется из 252 единиц белковых клеток, расположенных в определенной последовательности. В каждом углу икосаэдра расположены по 12 единиц белковых клеток в форме пятиугольной призмы и из этих углов простираются шипообразные структуры.

Впервые золотое сечение в строении вирусов обнаружили в 1950-хх гг. ученые из Лондонского Биркбекского Колледжа А.Клуг и Д.Каспар. 13 Первым логарифмическую форму явил в себе вирус Polyo. Форма этого вируса оказалась аналогичной с формой вируса Rhino 14.

Возникает вопрос, каким образом вирусы образуют столь сложные трехмерные формы, устройство которых содержит в себе золотое сечение, которые даже нашим человеческим умом сконструировать довольно сложно? Первооткрыватель этих форм вирусов, вирусолог А.Клуг дает такой комментарий:

Комментарий Клюга еще раз напоминает о предельно очевидной истине: в строении даже микроскопического организма, который ученые классифицируют как «самую примитивную форму жизни», в данном случае в вирусе, присутствует четкий замысел и осуществлен разумный проект 16. Этот проект несопоставим по своему совершенству и точности исполнения с самыми передовыми архитектурными проектами, созданными людьми. К примеру проектами, созданными гениальным архитектором Букминстером Фуллером.

Трехмерные модели додекаэдра и икосаэдра присутствуют также и в строении скелетов одноклеточных морских микроорганизмов радиолярий (лучевиков), скелет которых создан из кремнезёма.

Радиолярии формируют свое тело весьма изысканной, необычной красоты. Форма их составляет правильный додекаэдр. Причем из каждого его угла прорастает псевдоудлиннение-конечность и иные необычные формы-наросты.

В качестве примеров микроорганизмов, воплощающих в своем строении эти трехмерные геометрические фигуры, приведем Circigonia Icosahedra с икасаэдральным строением скелета и Circorhegma Dodecahedra с додекаэдральным строением скелета, причем размеры этих микроорганизмов не достигают и одного миллиметра.

МОДУЛЬ И МАСШТАБ

В греческой архитектуре только постройки архаической эпохи создают впечатление грандиозности массива. Это, по-видимому, зависит от самой громоздкости их пропорций.

Рассмотрим наиболее простой пример греческой конструкции, а именно антаблемент, не имеющий другой нагрузки, кроме собственной тяжести.

Анализ условий сопротивления показывает, что толщина этого антаблемента будет изменяться не в соответствии с увеличением пролета: так, при увеличении последнего в два раза она должна быть более чем удвоена. Другими словами, антаблемент крупных размеров оказывается более массивным, чем антаблемент над малыми пролетами.

Зато массивный антаблемент создает со своей стороны впечатление крупного сооружения, как например в храме Посейдонии, где преувеличенная массивность обусловливает иллюзию грандиозности здания.

Мы не будем утверждать, что такое преувеличение было преднамеренным, но создаваемое им впечатление является, по-видимому, присущим только архаическому периоду. Начиная с V в., греки обнаруживают стремление к оформлению ордеров, исходя из канона пропорций, не связанных с масштабом; мало-помалу они настолько поддаются влиянию этого метода, что поступаются ради установленных пропорций даже требованиями материальных удобств.

Нам представляется, например, что некоторые элементы архитектурного целого должны были бы сохранять, независимо от размеров здания, приблизительно одинаковый размер. Рассматривая проблему с чисто утилитарной точки зрения, казалось бы, что высота двери должна определяться исключительно высотой человеческого роста, а высота ступеней – сообразовываться с шагом человека, которому предстоит подниматься по ним.

Однако, если греки вообще руководствуются этими соображениями, то никак не далее архаического периода искусства, и очень скоро окончательно упускают их из вида. Они подчиняют постепенно размеры всех элементов здания модульному канону и увеличивают или уменьшают их в зависимости от увеличения или уменьшения модуля. Так, например, удваивая обмеры фасада, они одновременно удваивают высоту дверей и высоту ступеней. Исчезает всякая связь между назначением конструктивных частей и их размером; не остается ничего, что могло бы служить масштабом здания.

Архитекторы средневековья сумели согласовать пропорции, устанавливающие архитектурный ритм, с указаниями спасительного масштаба, дающего возможность определять размеры. Мы увидим, что установленный абсолютный размер определял разработку пропорций в частной архитектуре Рима.

Весьма возможно, что гражданская архитектура греков, если бы она дошла до нас в большей сохранности, также дала бы нам пример сооружений, где масштаб играл известную роль. Но в архитектуре храмов греки признают исключительно ритм. Их архитектурные произведения, по крайней мере относящиеся к последнему периоду, представляют собой как бы отвлеченную идею. Не связанные ни с чем, поддающимся измерению, они не вызывают никаких представлений об абсолютных величинах, а только чувство соотношений и впечатление гармонии.

Идеальный треугольник и пентаграмма

Идеальным называют равнобедренный треугольник, основание которого относится к длине стороны как 1/3. То есть, снова-таки соблюдается золотое сечение. Начертить треугольник с идеальным соотношением сторон несложно. Удобнее циркулем, но можно обойтись и линейкой.

Золотой треугольник, правило его построения и применение в создании интерьера, например

Построение такое. На прямой от точки A трижды откладываем отрезок произвольной длины. Эту длину обозначим O. Получаем точку B. Через нее проводим прямую, перпендикулярную отрезку AB. На этой линии в обе стороны от точки B откладываем величину O. Получаем две точки d и d1. Соединяем их с точкой A. Вот и получили треугольник, стороны которого относятся как 1,62. Проверить это можно, если отложить при помощи циркуля длину основания на боковой стороне (точка C). Вторая проверка — противолежащий угол составляет 36°.

Построение пентаграммы несколько сложнее. Ее вписываем в круг, без циркуля не обойтись.

• Центр окружности обозначаем O, через него проводим прямую до пересечения с окружностью. Одну из точек пересечения обозначаем A. Отрезок OA — диаметр окружности.
• Находим середину отрезка OD, ставим точку E. Из центра окружности вверх до пересечения с окружностью восстанавливаем перпендикуляр. Это точка D.

Построение пентаграммы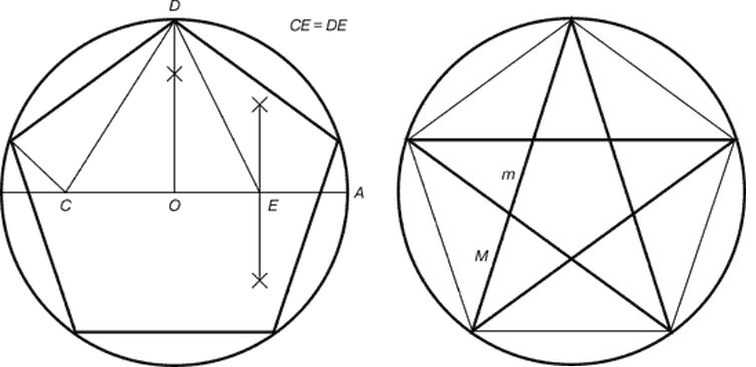

• Соединяем точки E и D. При помощи циркуля откладываем на радиусе точку C. Отрезок СD равен длине отрезка ED. Циркулем замеряем длину отрезка ED. Иглу ставим в точку E, ведем грифель до пересечения с радиусом. Вот и получили точку C.
• Длинна отрезка DC — сторона пентаграммы. Замеряем ее, при помощи циркуля переносим на окружность. Для этого циркулем с отложенным расстоянием ставим еще четыре точки на окружности, поочередно соединив их, получаем пентаграмму.

Вот что интересно, если вершины полученной пентаграммы использовать для прорисовки звезды, она будет состоять из идеальных треугольников.

Мифы и диковинные факты о пирамиде

Пирамида Хеопса также выстроена с учётом этого условия. Не вдаваясь в математическое доказательство наличия золотой формулы, скажем только, что в нём присутствуют прямоугольный золотой треугольник, сторонами которого являются высота и половина стороны основания строения. Ничего удивительного?

Но тогда возникает вопрос об уровне древнеегипетской математики. Выходит, что теорема Пифагора была им известна за два тысячелетия до рождения самого учёного

Внимание привлекает факт, что наследники Хеопса строили свои пирамиды уже с другими пропорциями. Почему?

Установлено, что сооружения пирамидальной формы с ЗС оказывают на находящихся в них феноменальное воздействие: растения лучше растут, металлы становятся прочнее, вода долго остаётся свежей. Учёные много лет работают с этими загадками, но тайна остаётся.

Замечено, что пирамида приводит структуру пространства в слаженное состояние. Всё, что попадает в зону действия, тоже организуется подобным образом: психоэмоциональное состояние людей улучшается, вредные для человека излучения уменьшаются, исчезают геопатогенные зоны. Интернет утверждает, что если размер фигуры увеличивается в два раза, то влияние пирамиды усиливается в сто раз.

Композиция в фотографии

Что же такое композиция и для чего она нужна в фотоискусстве? С помощью нее мы распределяем предметы и фигуры в пространстве снимка, устанавливаем определенные соотношения и размеры, учитываем тени, свет, цвета

Цель композиции — изобразить фотографируемые объекты определенным образом: привлечь к ним внимание, сделать их интереснее и показать с неожиданных сторон. В правильной композиции всегда будет “центр” кадра — объект, на который больше всего необходимо обратить внимание. Остальные же предметы и фигуры будут являться как бы фоном или менее значимыми элементами фотоснимка

Остальные же предметы и фигуры будут являться как бы фоном или менее значимыми элементами фотоснимка.

Композиционные правила

Есть несколько приемов, благодаря которым можно выстроить идеальную композицию в кадре. Они помогут правильно расставить акценты, выделить нужное, рассказать историю или передать эмоции и чувства.

Контрастность

Используется для того, чтобы привлечь максимальное внимание к нужному объекту. Предмет светлого оттенка разместите на более темном фоне, а темный — на светлом. Не стоит использовать пестрые фоны, которые будут забирать на себя большую часть внимания, а также сливаться с объектом

Не стоит использовать пестрые фоны, которые будут забирать на себя большую часть внимания, а также сливаться с объектом.

Грамотное размещение. Элементы кадры, которые важны фотографу, не следует размещать в кадре хаотично и как попало. Лучше, чтобы они образовывали геометрические фигуры — так будет гармоничнее.

Соблюдение пропорций. Если в кадре несколько объектов, которые стоят в разных частях и на нескольких планах, то фотографируйте таким образом, чтобы они соответствовали друг другу по размеру, объему и цветам.

Использование принципа золотого сечения. Коротко это правило гласит: лучше всего размещать объект на 1/3 от горизонтальной или вертикальной границы кадра.

Размещение по диагонали. Означает распределение объектов съемки вдоль по диагональным линиям, например, от левого верхнего края до правого нижнего. Так зритель пройдется взглядом по всей площади фотоснимка.

Формат фотографии

Вертикальные объекты, на которых вы акцентируете внимание, фотографируем вертикально. Для пейзажей подойдут горизонтальные кадры

Природа

Даже не вдаваясь в расчеты, золотое сечение можно без труда обнаружить в природе. Так, под него попадают соотношение хвоста и тела ящерицы, расстояния между листьями на ветке, есть золотое сечение и в форме яйца, если условную линию провести через его наиболее широкую часть.

Белорусский ученый Эдуард Сороко, который изучал формы золотых делений в природе, отмечал, что все растущее и стремящееся занять свое место в пространстве, наделено пропорциями золотого сечения. По его мнению, одна из самых интересных форм это закручивание по спирали.

Еще Архимед, уделяя внимание спирали, вывел на основе ее формы уравнение, которое и сейчас применяется в технике. Позднее Гете отмечал тяготение природы к спиральным формам, называя спираль «кривой жизни»

Современными учеными было установлено, что такие проявления спиральных форм в природе как раковина улитки, расположение семян подсолнечника, узоры паутины, движение урагана, строение ДНК и даже структура галактик заключают в себе ряд Фибоначчи.

Проектирование и создание макетов

Для создания успешных макетов необходимо учитывать два основных критерия: отдельные визуальные элементы и их взаимосвязь.

Существует множество вариантов построения макетов. Одним из них является расположение «Z». Оно показывает путь, который читатель проходит на странице. А также порядок, в котором он видит элементы.

Другой принцип компоновки – использование золотого сечения. Золотая спираль работает лучше всего, когда в дизайне большое количество элементов, которые могут отличаться друг от друга, но будут размещаться в одном макете

Внимание пользователей естественным образом притягиваются к центру спирали. Это позволяет разместить самый важный элемент в центре спирали

Идеальный треугольник и пентаграмма

Идеальным называют равнобедренный треугольник, основание которого относится к длине стороны как 1/3. То есть, снова-таки соблюдается золотое сечение. Начертить треугольник с идеальным соотношением сторон несложно. Удобнее циркулем, но можно обойтись и линейкой.

Золотой треугольник, правило его построения и применение в создании интерьера, например

Построение такое. На прямой от точки A трижды откладываем отрезок произвольной длины. Эту длину обозначим O. Получаем точку B. Через нее проводим прямую, перпендикулярную отрезку AB. На этой линии в обе стороны от точки B откладываем величину O. Получаем две точки d и d1. Соединяем их с точкой A. Вот и получили треугольник, стороны которого относятся как 1,62. Проверить это можно, если отложить при помощи циркуля длину основания на боковой стороне (точка C). Вторая проверка — противолежащий угол составляет 36°.

Построение пентаграммы несколько сложнее. Ее вписываем в круг, без циркуля не обойтись.

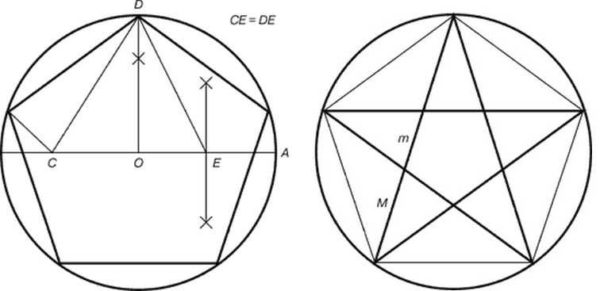
Вот что интересно, если вершины полученной пентаграммы использовать для прорисовки звезды, она будет состоять из идеальных треугольников.

https://youtube.com/watch?v=c3SVIQBXMnA

Математические свойства

• Φ{\displaystyle \Phi } — иррациональное алгебраическое число, положительное решение квадратного уравнения x2−x−1={\displaystyle x^{2}-x-1=0}, откуда, в частности, следуют соотношения:

  Φ2−Φ=1,{\displaystyle \Phi ^{2}-\Phi =1,}

  Φ⋅(Φ−1)=1.{\displaystyle \Phi \cdot (\Phi -1)=1.}

• Φ{\displaystyle \Phi } — представляется через тригонометрические функции:
  • Φ=2cos⁡π5=2cos⁡36∘.{\displaystyle \Phi =2\cos {\frac {\pi }{5}}=2\cos 36^{\circ }.}
  • Φ=2sin⁡(3π10)=2sin⁡54∘.{\displaystyle \Phi =2\sin(3\pi /10)=2\sin 54^{\circ }.}

1Φ=φ=tg⁡(arctg⁡(2)2)=21+1+22=21+5=5−12.{\displaystyle {\frac {1}{\Phi }}=\varphi =\operatorname {tg} \left({\frac {\operatorname {arctg} (2)}{2}}\right)={\frac {2}{1+{\sqrt {1+2^{2}}}}}={\frac {2}{1+{\sqrt {5}}}}={\frac {{\sqrt {5}}-1}{2}}.}

• Φ{\displaystyle \Phi } представляется в виде бесконечной цепочки квадратных корней:

  Φ=1+1+1+1+….{\displaystyle \Phi ={\sqrt {1+{\sqrt {1+{\sqrt {1+{\sqrt {1+\dots }}}}}}}}.}

• Φ{\displaystyle \Phi \;} представляется в виде бесконечной цепной дроби

  Φ=1+11+11+11+…,{\displaystyle \Phi =1+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{1+\dots }}}}}},}

подходящими дробями которой служат отношения последовательных чисел Фибоначчи Fn+1Fn{\displaystyle {\frac {F_{n+1}}{F_{n}}}}. Таким образом,

• Φ=limn→∞Fn+1Fn.{\displaystyle \Phi =\lim _{n\to \infty }{\frac {F_{n+1}}{F_{n}}}.}

• Мера иррациональности Φ{\displaystyle \Phi } равна 2.

Отрезание квадрата от прямоугольника, построенного по принципу золотого сечения

Отрезав квадрат от прямоугольника, построенного по принципу золотого сечения, мы получаем новый, уменьшенный прямоугольник с тем же отношением сторон Φ=a/b{\displaystyle \Phi =a/b}, что и у исходного прямоугольника Φ=(a+b)/a{\displaystyle \Phi =(a+b)/a}.

Золотое сечение в пятиконечной звезде

В правильной пятиконечной звезде каждый отрезок делится пересекающим его отрезком в золотом сечении. На приведённом рисунке отношения красного отрезка к зелёному, зелёного к синему и синего к пурпурному равны Φ{\displaystyle \Phi }. Кроме того, отношение красного отрезка к расстоянию между соседними вершинами звезды, которое равно зелёному отрезку, также равно Φ{\displaystyle \Phi }.

Построение золотого сечения

Геометрическое построение. Золотое сечение отрезка AB{\displaystyle AB} можно построить следующим образом: в точке B{\displaystyle B} восстанавливают перпендикуляр к AB{\displaystyle AB}, откладывают на нём отрезок BC{\displaystyle BC}, равный половине AB{\displaystyle AB}, на отрезке AC{\displaystyle AC} откладывают отрезок CD{\displaystyle CD}, равный BC{\displaystyle BC}, и наконец, на отрезке AB{\displaystyle AB} откладывают отрезок AE{\displaystyle AE}, равный AD{\displaystyle AD}. Тогда

Φ=|AB||AE|=|AE||BE|.{\displaystyle \Phi ={\frac {|AB|}{|AE|}}={\frac {|AE|}{|BE|}}.}

Другой способ построить отрезок, равный по длине числу золотого сечения

Другой способ построить отрезок, равный по длине числу золотого сечения, — начертить сначала квадрат ABCD со стороной 1. После этого одну из сторон, например сторону AD, разделить точкой E пополам, так что AE=DE=1/2. От точки B или C до точки E провести гипотенузу треугольника АВЕ или DCE. Согласно теореме Пифагора ВE=СE=52{\displaystyle {\frac {\sqrt {5}}{2}}}. Затем провести дугу с центром в точке Е от точки В или точки С до момента её пересечения с продолжением стороны АD (точкой пересечения дуги и продолжения стороны АD пусть будет точка Н). Как радиусы круга BE=СЕ=ЕН. Так как АН=АЕ+ЕН, результатом будет отрезок АН длиной Φ{\displaystyle \Phi }. Так как DH=EH-ED, другим результатом будет отрезок DH длиной φ{\displaystyle \varphi }.

• Отношение диагонали правильного пятиугольника к стороне равно золотому сечению.
• Значения дроби после запятой для Φ{\displaystyle \Phi }, 1Φ{\displaystyle {\frac {1}{\Phi }}} и Φ2{\displaystyle \Phi ^{2}} в любой системе счисления будут равны.
• ∑n=1∞(−1)n+1n2(2nn)=2ln2⁡φ{\displaystyle \sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n^{2}{\binom {2n}{n}}}}=2\ln ^{2}\varphi }

Тогда как ∑n=1∞1n2(2nn)=π218{\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{2}{\binom {2n}{n}}}}={\frac {\pi ^{2}}{18}}}[источник не указан 1010 дней]

Использование золотого сечения

Правило золотого сечения используются повсеместно. Когда человек постоянно передвигает мебель в доме, пытаясь найти то самое расположение, которое бы радовало глаз, он делает это подсознательно. Заложенная природой гармония пытается найти свое место в окружающем пространстве. Человек будет двигать, и переставлять мебель до тех пор, пока не придет к тому самому волшебному соотношению, к числу Фибоначчи, к золотым пропорциям.

Идеальное соотношение используется в архитектуре, в предметах быта, одежде, посуде. Например, столовый сервиз на 6 или 12 персон также можно рассматривать с точки зрения золотой пропорции. В ювелирных изделиях высокого качества, особенно в старинных украшениях ручной работы, четко прослеживается правильное соотношение.

В архитектурных памятниках законы золотых пропорций явственно просматриваются как в фасадах зданий, так и в окружающем ландшафте. Сады и парки Версаля, Петродворца, королевского Дворца в Марокко или Японии, — все построены в соответствии с законами золотого сечения. Великолепные композиции, продуманное расположение дорожек и архитектурных объектов призваны доставлять эстетическое удовольствие и радовать глаз своей гармонией.

Форма предмета и ее восприятие

Люди чаще всего ориентируются на форму предмета для того, чтобы распознавать его среди миллионов других. Именно по форме мы определяем, что за вещь лежит перед нами или стоит вдали. Мы в первую очередь узнаем людей по форме тела и лица. Поэтому с уверенностью можем утверждать, что сама форма, ее размеры и вид – одна из самых важных вещей в восприятии человека.

Для людей форма чего бы то ни было представляет интерес по двум главным причинам: либо это диктуется жизненной необходимостью, либо же вызывается эстетическим наслаждением от красоты. Самое лучшее зрительное восприятие и ощущение гармонии и красоты чаще всего приходит, когда человек наблюдает форму, в построении которой использовались симметрия и особое соотношение, которое и называется золотым сечением.

О пользе вальмовой крыши

Очень важным элементом архитектуры дома является крыша. Ее форма зависит, среди прочего, от величины пролета, то есть от ширины дома. Следует стремиться к тому, чтобы пролеты не были слишком большими. При ширине 12 м даже крыша с небольшим углом наклона скатов выглядит громоздко. А при ширине 9 м такая же крыша может быть выше и заметнее, при этом ее конструкция будет проще. Особенно нам нравятся вальмовые крыши с широкими карнизными свесами и углом наклона скатов около 40°.

Двухэтажный дом с вальмовой, простой крышей был запроектирован для участка с въездом с южной стороны

Для того чтобы не «потерять» солнечный участок, гараж и хозяйственную часть разместили за домом.

Вальмовая крыша прекрасно завершает объем, венчая все стены. Дом с такой крышей выглядит спокойно и единообразно с любой точки. А вот дом с двухскатной крышей выглядит по-разному с разных точек: со стороны щипцовой стены — это один образ, со стороны фасадов — другой. Иногда эти образы отличаются так, что создают впечатление диссонанса. Вальмовая крыша является индикатором сбалансированности проекта: если ее контур является замкнутым прямоугольником, а края скатов сходятся в соответствующей точке — это наилучшее доказательство того, что с формой дома все в порядке. Естественно, у вальмовой крыши есть и недостатки. Ей необходимо больше опор, расположение которых нужно продумать, учитывая не только конструктивные требования, но и удобство планировки помещений. На такой крыше плохо смотрятся многочисленные мансардные окна и дымоходы.

На мансарде под вальмовой крышей больше скатов, чем под двухскатной, следовательно дизайн внутреннего пространства будет сложнее. Ее непросто проектировать и выполнять. Однако именно благодаря такой форме крыши, дом имеет замкнутый объем, спокойный и упорядоченный образ.

Божественная пропорция: что создано природой

Обратимся к природе, которая является безусловной и стремится к идеальному. В любом, созданном процессе, можно наблюдать эту магическую пропорцию 62:38. Придя к выводу, что гармоничное восприятие заложено в человеке от природы, ученые назвали это соотношение «Божественная пропорция».

Архимед выразил ее в спирали, повторяющей очертания раковины моллюска, подметив однажды ее идеальные формы. Божественная пропорция в архитектуре выражена с помощью сопоставления различных элементов здания и приведения их к одному целому, гармоничному для восприятия.

Действительно, обычно притягивает взгляд либо совершенство, либо уродство. И то и другое имеет одни корни

Совершенство – созданный по системе золотой пропорции идеал, и неважно, искусственный или природный источник использовался в его создании. Уродство же, напротив, привлекает полным несоответствием гармонии, что вынуждает подсознательно искать в нем заложенные природой прекрасные пропорции

И, если постараться, их можно найти. Этот феномен будоражит мозг, заставляя искать спокойной геометрии во всем.

Как использовать Золотое Сечение

Использовать этот принцип проще, чем вы думаете. Существует пара быстрых трюков, которые вы можете использовать в своих макетах, или потратить немного больше времени и полностью раскрыть концепт.

Быстрый способ

Если вы когда-нибудь сталкивались с “Правилом третей”, то вам будет знакома идея разделения пространства на равные трети по вертикали и горизонтали, при этом места пересечения линий создают естественные точки для объектов.

Фотограф размещает ключевой объект на одной из этих пересекающихся линий, чтобы создать приятную композицию. Этот прицип может также использоваться в вашей разметке страниц и дизайне постеров.

Правило третей можно применять к любой форме, но если вы примените его к прямоугольнику с пропорциями примерно 1 : 1.6, вы окажетесь очень близко к золотому прямоугольнику, что сделает композицию более приятной для глаз.

Полная реализация

Если вы хотите реализовать Золотое Сечение в вашем дизайне в полной мере, то просто расположите основной контент и сайдбар (в веб дизайне) в соотношении равном 1 : 1.61.

Можно округлить значения в меньшую или большую стороны: если контент-зона равна 640px, а сайдбар 400px, то эта разметка вполне подойдет под Золотое Сечение.

Разумеется, вы также можете разделить области контента и боковой панели на одно и то же отношение, а связь между заголовком веб-страницы, областью содержимого, футером и навигацией также может быть спроектирована с использованием того же приципа.